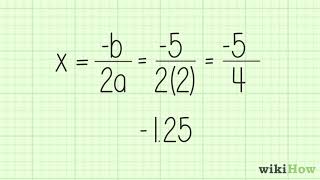In Exercises 39–44, an equation of a quadratic function is given. a) Determine, without graphing, whether the function has a minimum value or a maximum value. b) Find the minimum or maximum value and determine where it occurs. c) Identify the function's domain and its range. f(x)=5x^2−5x

Verified step by step guidance

1. <Step 1: Identify the form of the quadratic function. The given function is f(x) = 5x^2 - 5x, which is in the standard form of a quadratic function, ax^2 + bx + c. Here, a = 5, b = -5, and c = 0.>
2. <Step 2: Determine whether the function has a minimum or maximum value. Since the coefficient of x^2 (a = 5) is positive, the parabola opens upwards, indicating that the function has a minimum value.>
3. <Step 3: Find the vertex of the parabola, which gives the minimum value. The x-coordinate of the vertex can be found using the formula x = -b/(2a). Substitute b = -5 and a = 5 into the formula to find the x-coordinate of the vertex.>
4. <Step 4: Calculate the minimum value of the function by substituting the x-coordinate of the vertex back into the function f(x). This will give you the minimum value of the function.>
5. <Step 5: Determine the domain and range of the function. The domain of any quadratic function is all real numbers, (-∞, ∞). Since the parabola opens upwards and has a minimum value, the range is [minimum value, ∞).>

Key Concepts

Quadratic Functions

A quadratic function is a polynomial function of degree two, typically expressed in the form f(x) = ax^2 + bx + c. The coefficient 'a' determines the direction of the parabola: if 'a' is positive, the parabola opens upwards, indicating a minimum value; if 'a' is negative, it opens downwards, indicating a maximum value.

Vertex of a Parabola

The vertex of a parabola is the highest or lowest point on the graph, depending on whether it opens upwards or downwards. For a quadratic function in standard form, the vertex can be found using the formula x = -b/(2a). The y-coordinate of the vertex gives the maximum or minimum value of the function.

Domain and Range

The domain of a function refers to all possible input values (x-values) for which the function is defined, while the range refers to all possible output values (y-values). For quadratic functions, the domain is typically all real numbers, and the range depends on the vertex: if the parabola opens upwards, the range starts from the minimum value to positive infinity; if it opens downwards, it extends from negative infinity to the maximum value.