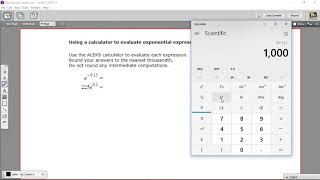
In Exercises 11–18, graph each function by making a table of coordinates. If applicable, use a graphing utility to confirm your hand-drawn graph. h(x) = (1/2)^x

Key Concepts

Exponential Functions

Exponential functions are mathematical expressions in the form of f(x) = a^x, where 'a' is a positive constant. In this case, h(x) = (1/2)^x represents a decreasing exponential function because the base (1/2) is less than 1. Understanding the behavior of exponential functions is crucial for predicting how they will graphically appear, particularly their rapid decrease as x increases.

Table of Coordinates

Creating a table of coordinates involves selecting various values for x and calculating the corresponding values of h(x). This process helps in plotting points on a graph, providing a visual representation of the function's behavior. For h(x) = (1/2)^x, you would typically choose a range of x values, including negative, zero, and positive numbers, to observe how the function behaves across different intervals.

Graphing Utilities

Graphing utilities are software tools or calculators that allow users to visualize mathematical functions quickly and accurately. They can confirm the results obtained from hand-drawn graphs by providing a precise graphical representation of the function. Using a graphing utility for h(x) = (1/2)^x can help verify the shape and key features of the graph, such as the horizontal asymptote and the rate of decrease.