Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
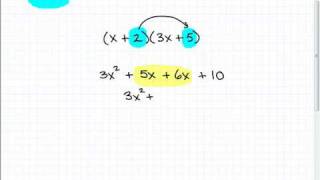
Multiplying Polynomials
Problem 127
Textbook Question
In Exercises 117–130, simplify each algebraic expression. 7-4[3-(4y-5)]
 Verified step by step guidance
Verified step by step guidance1
Start by simplifying the expression inside the innermost parentheses: \(3 - (4y - 5)\).
Distribute the negative sign across the terms inside the parentheses: \(3 - 4y + 5\).
Combine like terms inside the brackets: \(3 + 5 - 4y\) simplifies to \(8 - 4y\).
Substitute back into the original expression: \(7 - 4[8 - 4y]\).
Distribute the \(-4\) across the terms inside the brackets: \(7 - 4 \times 8 + 4 \times 4y\).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Order of Operations
The order of operations is a set of rules that dictates the sequence in which mathematical operations should be performed to ensure consistent results. The acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) helps remember this order. In the given expression, operations within parentheses must be simplified first, followed by multiplication and subtraction.
Recommended video:
Guided course

Performing Row Operations on Matrices
Distributive Property
The distributive property states that a(b + c) = ab + ac, allowing us to multiply a single term by each term within a set of parentheses. This property is essential for simplifying expressions that involve multiplication of a term with a sum or difference. In the expression provided, applying the distributive property will help simplify the term 4[3 - (4y - 5)].
Recommended video:
Guided course

Multiply Polynomials Using the Distributive Property
Combining Like Terms
Combining like terms involves simplifying expressions by adding or subtracting terms that have the same variable raised to the same power. This process is crucial for reducing expressions to their simplest form. After applying the order of operations and the distributive property in the given expression, combining like terms will help finalize the simplification.
Recommended video:

Combinations
Related Videos
Related Practice