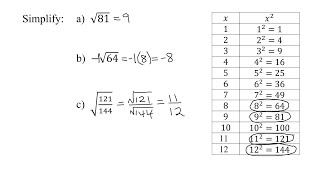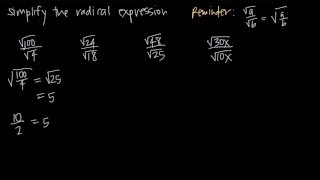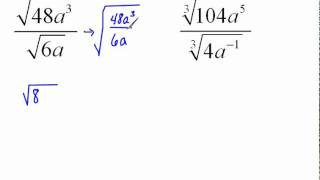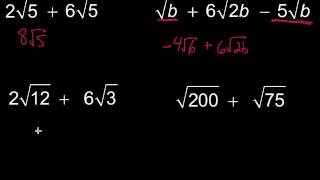Simplify each exponential expression in Exercises 23–64. (x^11)^5

Key Concepts

Exponential Rules

Exponential rules are mathematical principles that govern the operations involving exponents. One key rule is the power of a power rule, which states that when raising a power to another power, you multiply the exponents. For example, (a^m)^n = a^(m*n). This rule is essential for simplifying expressions like (x^11)^5.

Base and Exponent

In exponential expressions, the base is the number being multiplied, while the exponent indicates how many times the base is used as a factor. For instance, in x^11, x is the base and 11 is the exponent. Understanding the roles of base and exponent is crucial for correctly applying the rules of exponents during simplification.

Simplification of Expressions

Simplification involves rewriting an expression in a more concise or manageable form without changing its value. In the context of exponents, this often means applying the rules of exponents to reduce the expression to its simplest form. For example, simplifying (x^11)^5 results in x^(11*5) = x^55, demonstrating the process of simplification.