Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
5. Rational Functions
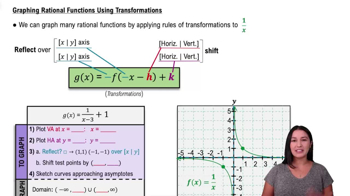
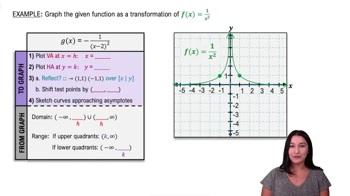
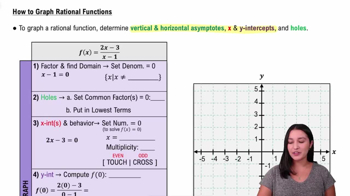
Graphing Rational Functions
Problem 107
Textbook Question
Find a rational function ƒ having a graph with the given features. x-intercepts: (-1, 0) and (3, 0) y-intercept: (0, -3) vertical asymptote: x=1 horizontal asymptote: y=1
 Verified step by step guidance
Verified step by step guidance1
Identify the factors for the numerator from the x-intercepts. Since the x-intercepts are (-1, 0) and (3, 0), the factors are (x + 1) and (x - 3). Thus, the numerator of the rational function can be written as (x + 1)(x - 3).
Determine the denominator from the vertical asymptote. The vertical asymptote at x = 1 suggests a factor in the denominator that becomes zero at x = 1, which is (x - 1).
Use the y-intercept to find the constant that will multiply the numerator. The y-intercept is given as (0, -3). Substitute x = 0 into the rational function and set the output equal to -3 to solve for the constant k: f(0) = k(0 + 1)(0 - 3)/(0 - 1) = -3.
Incorporate the horizontal asymptote into the function. A horizontal asymptote at y = 1 suggests that the degrees of the numerator and denominator are equal, and the leading coefficients' ratio is 1. Ensure the function adheres to this by adjusting the numerator and denominator if necessary.
Combine all the information to write the rational function. The function should now be structured to include the correct factors in the numerator and denominator, the constant k, and should reflect the horizontal asymptote correctly.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
10mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rational Functions
A rational function is a function that can be expressed as the ratio of two polynomials. It typically takes the form f(x) = P(x)/Q(x), where P and Q are polynomials. Understanding the structure of rational functions is essential for analyzing their behavior, including intercepts and asymptotes.
Recommended video:

Intro to Rational Functions
Intercepts
Intercepts are points where a graph crosses the axes. The x-intercepts occur where the function equals zero, while the y-intercept is found by evaluating the function at x=0. Identifying these points is crucial for sketching the graph of the rational function and understanding its roots.
Recommended video:
Guided course

Graphing Intercepts
Asymptotes
Asymptotes are lines that the graph of a function approaches but never touches. Vertical asymptotes occur where the denominator of a rational function is zero, indicating undefined values. Horizontal asymptotes describe the behavior of the function as x approaches infinity, providing insight into the function's end behavior.
Recommended video:

Introduction to Asymptotes

 5:31m
5:31mWatch next
Master Graphing Rational Functions Using Transformations with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice