Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
5. Rational Functions
Graphing Rational Functions
Problem 107
Textbook Question
Textbook QuestionFind a rational function ƒ having a graph with the given features. x-intercepts: (-1, 0) and (3, 0) y-intercept: (0, -3) vertical asymptote: x=1 horizontal asymptote: y=1
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
10mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rational Functions
A rational function is a function that can be expressed as the ratio of two polynomials. It typically takes the form f(x) = P(x)/Q(x), where P and Q are polynomials. Understanding the structure of rational functions is essential for analyzing their behavior, including intercepts and asymptotes.
Recommended video:
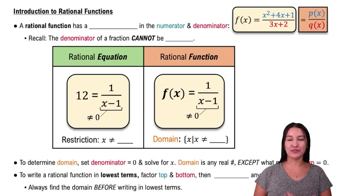
Intro to Rational Functions
Intercepts
Intercepts are points where a graph crosses the axes. The x-intercepts occur where the function equals zero, while the y-intercept is found by evaluating the function at x=0. Identifying these points is crucial for sketching the graph of the rational function and understanding its roots.
Recommended video:
Guided course

Graphing Intercepts
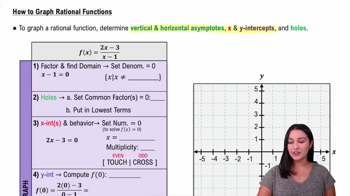
Asymptotes
Asymptotes are lines that the graph of a function approaches but never touches. Vertical asymptotes occur where the denominator of a rational function is zero, indicating undefined values. Horizontal asymptotes describe the behavior of the function as x approaches infinity, providing insight into the function's end behavior.
Recommended video:

Introduction to Asymptotes

 5:31m
5:31mWatch next
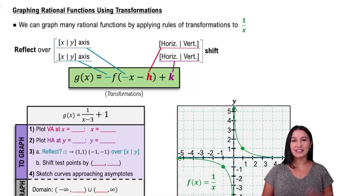
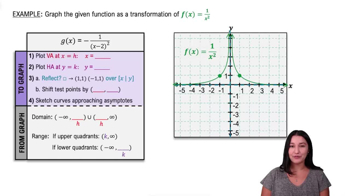
Master Graphing Rational Functions Using Transformations with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice