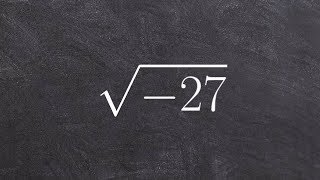Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
1. Equations & Inequalities
The Imaginary Unit
Problem 69
Textbook Question
Find each product. Write answers in standard form. 3i(2-i)²
 Verified step by step guidance
Verified step by step guidance1
Step 1: First, we need to simplify the expression inside the parentheses. The expression (2-i)² means (2-i) multiplied by itself. So, we have to multiply (2-i) by (2-i).
Step 2: To multiply two complex numbers, we use the distributive property, also known as the FOIL method. This stands for First, Outer, Inner, Last. So, we multiply the first terms (2*2), the outer terms (2*-i), the inner terms (-i*2), and the last terms (-i*-i).
Step 3: After performing the multiplication, we simplify the result. Remember that i² = -1.
Step 4: Now, we have a simplified expression inside the parentheses. The next step is to multiply this result by 3i.
Step 5: Finally, we simplify the result to get the product in standard form. The standard form of a complex number is a + bi, where a and b are real numbers, and i is the imaginary unit.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Complex Numbers
Complex numbers are numbers that have a real part and an imaginary part, expressed in the form a + bi, where 'a' is the real part and 'b' is the coefficient of the imaginary unit 'i', which is defined as the square root of -1. Understanding complex numbers is essential for performing operations involving them, such as addition, subtraction, multiplication, and division.
Recommended video:

Dividing Complex Numbers
Exponentiation
Exponentiation is a mathematical operation involving two numbers, the base and the exponent, where the base is multiplied by itself as many times as indicated by the exponent. In the expression (2 - i)², it is crucial to apply the exponent correctly, which involves multiplying (2 - i) by itself to simplify the expression before further operations.
Recommended video:

Exponential Functions
Standard Form of Complex Numbers
The standard form of a complex number is expressed as a + bi, where 'a' and 'b' are real numbers. When multiplying complex numbers, the result should be simplified to this form, ensuring that the imaginary unit 'i' is properly accounted for and that any like terms are combined to present the final answer clearly.
Recommended video:

Multiplying Complex Numbers

 5:02m
5:02mWatch next
Master Square Roots of Negative Numbers with a bite sized video explanation from Callie
Start learning