Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
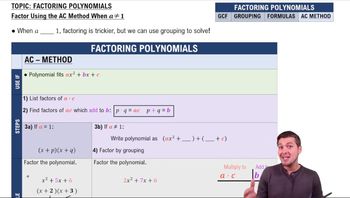
Factoring Polynomials
Problem 101
Textbook Question
Textbook QuestionFactor by any method. See Examples 1–7. 4z^2+28z+49
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Factoring Quadratic Expressions
Factoring quadratic expressions involves rewriting a polynomial in the form ax^2 + bx + c as a product of two binomials. This process is essential for simplifying expressions and solving equations. For example, the expression 4z^2 + 28z + 49 can be factored to identify its roots and analyze its graph.
Recommended video:

Solving Quadratic Equations by Factoring
Perfect Square Trinomials
A perfect square trinomial is a specific type of quadratic expression that can be expressed as the square of a binomial. The general form is (a + b)^2 = a^2 + 2ab + b^2. In the case of 4z^2 + 28z + 49, recognizing it as a perfect square trinomial allows us to factor it as (2z + 7)^2.
Recommended video:

Solving Quadratic Equations by Completing the Square
The Distributive Property
The distributive property states that a(b + c) = ab + ac, which is fundamental in both expanding and factoring expressions. When factoring, we often reverse this property to find common factors or to express a polynomial as a product of simpler expressions. Understanding this property is crucial for manipulating algebraic expressions effectively.
Recommended video:
Guided course

Multiply Polynomials Using the Distributive Property

 7:30m
7:30mWatch next
Master Introduction to Factoring Polynomials with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice