Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Function Operations
Problem 34
Textbook Question
Use the graph to evaluate each expression. See Example 3(a). (ƒ-g)(-1) 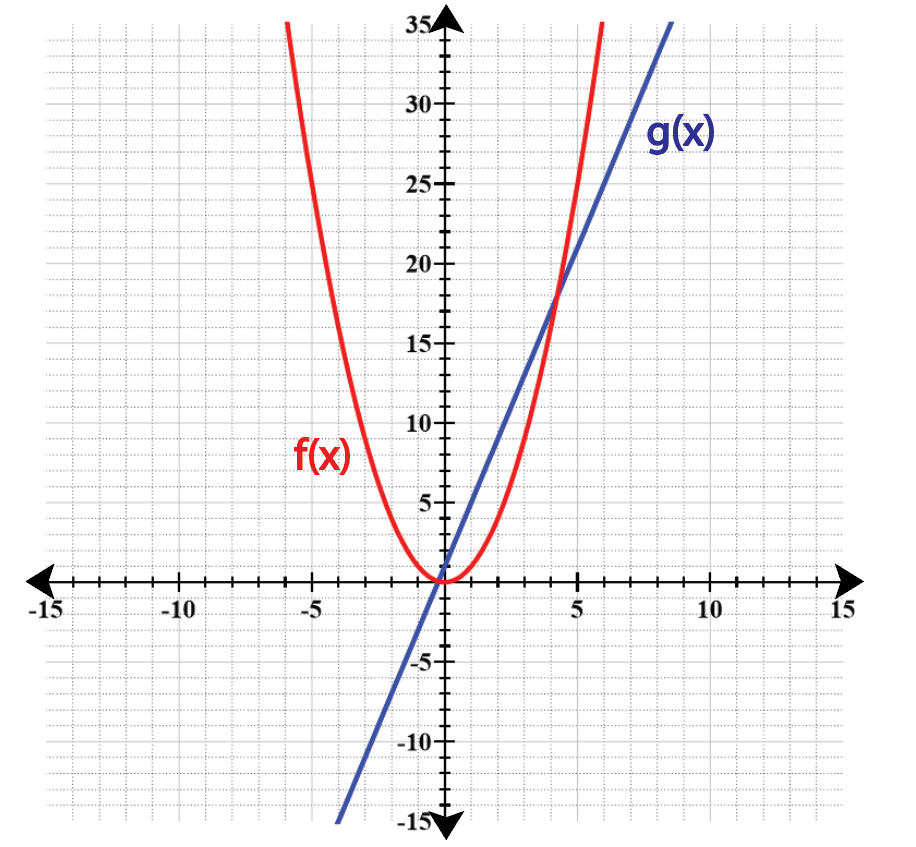
 Verified step by step guidance
Verified step by step guidance1
Identify the functions \( f(x) \) and \( g(x) \) from the graph. \( f(x) \) is the red parabola and \( g(x) \) is the blue line.
Locate the point \( x = -1 \) on the x-axis and find the corresponding y-values for both \( f(x) \) and \( g(x) \).
Read the y-value of \( f(x) \) at \( x = -1 \) from the graph.
Read the y-value of \( g(x) \) at \( x = -1 \) from the graph.
Subtract the y-value of \( g(x) \) from the y-value of \( f(x) \) to evaluate \((f-g)(-1)\).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Function Evaluation
Function evaluation involves substituting a specific input value into a function to determine its output. For example, if f(x) is a function, evaluating f(-1) means finding the value of the function when x equals -1. This is crucial for understanding how to compute values from the graph of the functions f(x) and g(x).
Recommended video:

Evaluating Composed Functions
Graph Interpretation
Graph interpretation is the ability to read and analyze graphical representations of functions. In this context, it involves identifying the values of f(-1) and g(-1) from the graph, which are necessary for calculating (f-g)(-1). Understanding how to extract information from the graph is essential for solving the problem.
Recommended video:
Guided course

Graphs and Coordinates - Example
Function Subtraction
Function subtraction refers to the operation of subtracting the output of one function from another. In this case, (f-g)(x) means taking the value of f(x) and subtracting g(x) from it. To evaluate (f-g)(-1), one must first find f(-1) and g(-1) and then perform the subtraction, which is a fundamental operation in algebra.
Recommended video:

Adding & Subtracting Functions

 5:56m
5:56mWatch next
Master Adding & Subtracting Functions with a bite sized video explanation from Nick Kaneko
Start learning


