Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Multiplying Polynomials
Problem 53c
Textbook Question
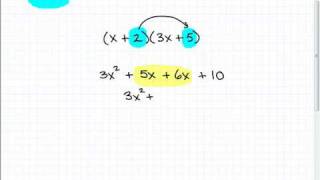
In Exercises 35–54, use the FOIL method to multiply the binomials. (3xⁿ−yⁿ)(xⁿ+2yⁿ)
 Verified step by step guidance
Verified step by step guidance1
Identify the binomials to be multiplied: \((3x^n - y^n)\) and \((x^n + 2y^n)\).
Apply the FOIL method, which stands for First, Outer, Inner, Last, to multiply the binomials.
First: Multiply the first terms of each binomial: \(3x^n \cdot x^n\).
Outer: Multiply the outer terms of the binomials: \(3x^n \cdot 2y^n\).
Inner: Multiply the inner terms of the binomials: \(-y^n \cdot x^n\).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
FOIL Method
The FOIL method is a technique used to multiply two binomials. It stands for First, Outside, Inside, Last, referring to the order in which you multiply the terms. This method helps ensure that all combinations of the terms are accounted for, leading to the correct expansion of the expression.
Recommended video:
Binomials
A binomial is a polynomial that consists of exactly two terms, which can be separated by a plus or minus sign. In the expression (3xⁿ−yⁿ)(xⁿ+2yⁿ), both factors are binomials. Understanding how to manipulate binomials is essential for performing operations like multiplication and factoring in algebra.
Recommended video:
Guided course

Special Products - Cube Formulas
Polynomial Expansion
Polynomial expansion involves distributing each term in one polynomial to every term in another polynomial. This process results in a new polynomial that combines like terms. Mastery of polynomial expansion is crucial for simplifying expressions and solving equations in algebra.
Recommended video:
Guided course

Introduction to Polynomials
Related Videos
Related Practice