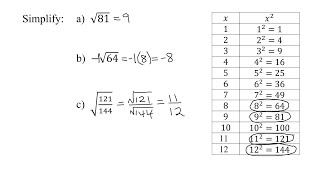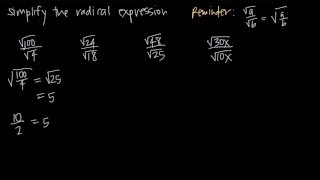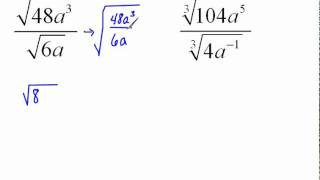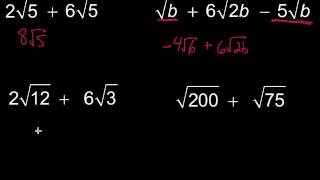Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Radical Expressions
Problem 48b
Textbook Question
Textbook QuestionIn Exercises 39–64, rationalize each denominator. 10 ----- ³√5
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rationalizing the Denominator
Rationalizing the denominator involves rewriting a fraction so that the denominator is a rational number. This is often necessary when the denominator contains a radical, such as a square root or cube root. The goal is to eliminate the radical from the denominator, making the expression easier to work with and understand.
Recommended video:
Guided course

Rationalizing Denominators
Cube Roots
A cube root of a number is a value that, when multiplied by itself three times, gives the original number. For example, the cube root of 8 is 2, since 2 × 2 × 2 = 8. In the context of rationalizing denominators, understanding how to manipulate cube roots is essential for simplifying expressions that involve them.
Recommended video:

Imaginary Roots with the Square Root Property
Multiplying by the Conjugate
When rationalizing denominators that contain roots, one common technique is to multiply both the numerator and the denominator by a form of the conjugate. For cube roots, this involves using a specific factor that will eliminate the radical when multiplied. This method ensures that the overall value of the fraction remains unchanged while simplifying the expression.
Recommended video:

Complex Conjugates
Related Videos
Related Practice