Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Factoring Polynomials
Problem 69b
Textbook Question
Textbook QuestionIn Exercises 69–80, factor completely. x⁴ − 5x²y² + y⁴
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
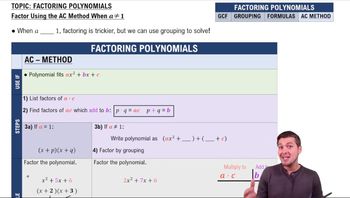
Factoring Polynomials
Factoring polynomials involves rewriting a polynomial as a product of simpler polynomials or factors. This process is essential for simplifying expressions and solving equations. In the case of the expression x⁴ − 5x²y² + y⁴, recognizing it as a quadratic in terms of x² can facilitate the factoring process.
Recommended video:
Guided course

Introduction to Factoring Polynomials
Difference of Squares
The difference of squares is a specific factoring technique used when an expression takes the form a² - b², which can be factored into (a - b)(a + b). In the given polynomial, recognizing patterns that resemble the difference of squares can help in breaking down the expression into simpler factors.
Recommended video:

Solving Quadratic Equations by Completing the Square
Quadratic Form
A quadratic form is an expression that can be rewritten in the standard quadratic form ax² + bx + c. In this case, the expression x⁴ − 5x²y² + y⁴ can be treated as a quadratic in x², allowing us to apply techniques for factoring quadratics, such as completing the square or using the quadratic formula.
Recommended video:

Vertex Form

 7:30m
7:30mWatch next
Master Introduction to Factoring Polynomials with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice