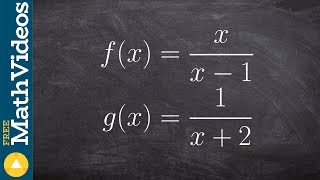For the pair of functions defined, find (ƒ/g)(x). Give the domain of each. See Example 2. ƒ(x)=2x^2-3x, g(x)=x^2-x+3

Verified step by step guidance

1. Step 1: Understand that (ƒ/g)(x) represents the division of the function ƒ(x) by the function g(x), which is expressed as (ƒ/g)(x) = ƒ(x) / g(x).
2. Step 2: Substitute the given functions into the expression: (ƒ/g)(x) = (2x^2 - 3x) / (x^2 - x + 3).
3. Step 3: Identify the domain of the function (ƒ/g)(x). The domain consists of all real numbers except those that make the denominator zero.
4. Step 4: Set the denominator equal to zero and solve for x: x^2 - x + 3 = 0. Use the quadratic formula if necessary to find the values of x that are not in the domain.
5. Step 5: Conclude that the domain of (ƒ/g)(x) is all real numbers except the solutions found in Step 4, as these would make the denominator zero and the function undefined.

Key Concepts

Function Division

Function division involves creating a new function by dividing one function by another. In this case, (ƒ/g)(x) means we take the function ƒ(x) and divide it by g(x). This operation requires understanding how to manipulate algebraic expressions and the implications of division, particularly regarding the domain of the resulting function.

Domain of a Function

The domain of a function is the set of all possible input values (x-values) for which the function is defined. For rational functions, the domain is restricted by any values that make the denominator zero, as division by zero is undefined. Therefore, when finding the domain of (ƒ/g)(x), we must identify the values of x that make g(x) equal to zero and exclude them from the domain.

Polynomial Functions

Polynomial functions are expressions that consist of variables raised to non-negative integer powers and their coefficients. In this question, both ƒ(x) and g(x) are polynomial functions. Understanding their structure helps in performing operations like addition, subtraction, multiplication, and division, as well as analyzing their behavior, such as finding roots and determining the domain.