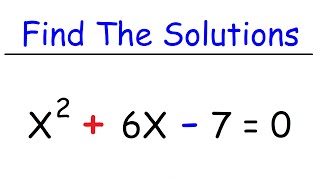Exercises 82–84 will help you prepare for the material covered in the next section. Solve: x^2+4x+6=0

Verified step by step guidance

1. <Step 1: Identify the type of equation.> The given equation is a quadratic equation of the form \( ax^2 + bx + c = 0 \), where \( a = 1 \), \( b = 4 \), and \( c = 6 \).
2. <Step 2: Determine the method to solve the quadratic equation.> Since the equation does not factor easily, use the quadratic formula: \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \).
3. <Step 3: Calculate the discriminant.> Compute \( b^2 - 4ac \) to determine the nature of the roots. Substitute \( b = 4 \), \( a = 1 \), and \( c = 6 \) into the discriminant formula: \( 4^2 - 4 \times 1 \times 6 \).
4. <Step 4: Evaluate the discriminant.> Simplify the expression \( 16 - 24 \) to find the value of the discriminant.
5. <Step 5: Analyze the discriminant.> Since the discriminant is negative, the quadratic equation has two complex conjugate roots. Proceed to use the quadratic formula to find these roots.

Key Concepts

Quadratic Equations

A quadratic equation is a polynomial equation of the form ax^2 + bx + c = 0, where a, b, and c are constants, and a ≠ 0. The solutions to these equations can be found using various methods, including factoring, completing the square, or applying the quadratic formula. Understanding the structure of quadratic equations is essential for solving them.

The Quadratic Formula

The quadratic formula, x = (-b ± √(b² - 4ac)) / (2a), provides a method for finding the roots of any quadratic equation. The term under the square root, known as the discriminant (b² - 4ac), determines the nature of the roots: if it's positive, there are two distinct real roots; if zero, one real root; and if negative, two complex roots. This formula is crucial for solving the given equation.

Completing the Square

Completing the square is a method used to solve quadratic equations by rewriting them in the form (x + p)² = q. This technique involves manipulating the equation to create a perfect square trinomial, which can then be solved easily. It is particularly useful when the quadratic formula is not preferred or when deriving the vertex form of a parabola.