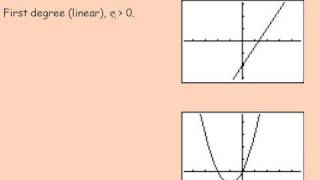
Use an end behavior diagram, , , , or , to describe the end behavior of the graph of each polynomial function. See Example 2. ƒ(x)=3+2x-4x^2-5x^10

Key Concepts

End Behavior of Polynomials

The end behavior of a polynomial function describes how the function behaves as the input values (x) approach positive or negative infinity. This behavior is primarily determined by the leading term of the polynomial, which is the term with the highest degree. Depending on the degree and the leading coefficient, the graph will either rise or fall at the ends.

Leading Coefficient Test

The leading coefficient test helps predict the end behavior of a polynomial function based on the sign and degree of the leading term. If the leading coefficient is positive and the degree is even, the ends of the graph will rise; if the degree is odd, one end will rise and the other will fall. Conversely, if the leading coefficient is negative, the behavior is reversed.

Degree of a Polynomial

The degree of a polynomial is the highest exponent of the variable in the polynomial expression. It plays a crucial role in determining the shape and end behavior of the graph. For example, a polynomial of even degree can have a different end behavior compared to one of odd degree, influencing how the graph approaches infinity.