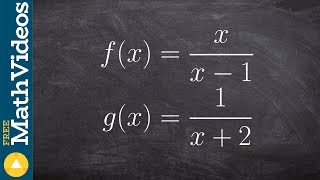If (fg)(x) = 4x²−x−5, find f and g.

Verified step by step guidance

1. Step 1: Understand that (fg)(x) represents the product of two functions f(x) and g(x). We need to find two functions whose product is 4x^2 - x - 5.
2. Step 2: Consider the structure of the quadratic expression 4x^2 - x - 5. It can be factored into two binomials, which will represent f(x) and g(x).
3. Step 3: Use the method of factoring quadratics to express 4x^2 - x - 5 as a product of two binomials. Look for two numbers that multiply to the product of the leading coefficient (4) and the constant term (-5), which is -20, and add to the middle coefficient (-1).
4. Step 4: Once you find the two numbers, rewrite the middle term (-x) using these numbers, and then factor by grouping.
5. Step 5: After factoring by grouping, you will have the expression in the form (ax + b)(cx + d), where f(x) = ax + b and g(x) = cx + d.

Key Concepts

Function Composition

Function composition involves combining two functions, f and g, to create a new function, denoted as (fg)(x). This means that the output of g becomes the input for f. Understanding how to manipulate and decompose composite functions is essential for solving problems that require finding the original functions from their product.

Factoring Quadratic Expressions

Factoring quadratic expressions, such as 4x²−x−5, is a key algebraic skill that involves rewriting the expression as a product of two binomials. This process helps in identifying the roots of the quadratic and can also assist in determining the functions f and g when the product of these functions is given.

Identifying Function Types

Recognizing the types of functions involved, such as linear, quadratic, or polynomial functions, is crucial for determining possible forms of f and g. In this case, since the product is a quadratic expression, both f and g are likely to be linear functions, which can be expressed in the form f(x) = ax + b and g(x) = cx + d.