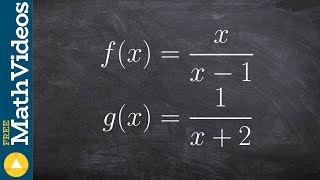Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Function Composition
Problem 102
Textbook Question
Textbook QuestionIf (fg)(x) = 4x²−x−5, find f and g.
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Function Composition
Function composition involves combining two functions, f and g, to create a new function, denoted as (fg)(x). This means that the output of g becomes the input for f. Understanding how to manipulate and decompose composite functions is essential for solving problems that require finding the original functions from their product.
Recommended video:

Function Composition
Factoring Quadratic Expressions
Factoring quadratic expressions, such as 4x²−x−5, is a key algebraic skill that involves rewriting the expression as a product of two binomials. This process helps in identifying the roots of the quadratic and can also assist in determining the functions f and g when the product of these functions is given.
Recommended video:

Solving Quadratic Equations by Factoring
Identifying Function Types
Recognizing the types of functions involved, such as linear, quadratic, or polynomial functions, is crucial for determining possible forms of f and g. In this case, since the product is a quadratic expression, both f and g are likely to be linear functions, which can be expressed in the form f(x) = ax + b and g(x) = cx + d.
Recommended video:
Guided course

Types of Slope

 4:56m
4:56mWatch next
Master Function Composition with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice