Here are the essential concepts you must grasp in order to answer the question correctly.
Piecewise Functions
A piecewise function is defined by different expressions based on the input value. Each segment of the function applies to a specific interval of the domain, allowing for varied behavior in different regions. Understanding how to interpret and graph these functions is crucial, as it involves determining which expression to use based on the value of x.
Recommended video:
Graphing Techniques
Graphing piecewise functions requires plotting each segment separately according to its defined conditions. This involves identifying the endpoints and whether they are included (closed dot) or excluded (open dot) in the graph. Mastery of graphing techniques is essential for accurately representing the function visually and understanding its behavior at transition points.
Recommended video:
Graphs and Coordinates - Example
Continuity and Discontinuity
Continuity refers to a function being unbroken and having no gaps at a point, while discontinuity indicates a break or jump in the function's graph. When dealing with piecewise functions, it is important to analyze the points where the function changes from one expression to another to determine if the function is continuous or if there are any jumps or holes in the graph.
Recommended video:
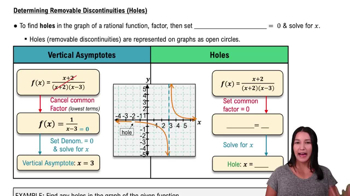
Determining Removable Discontinuities (Holes)

 Verified step by step guidance
Verified step by step guidance Verified Solution
Verified Solution


 5:2m
5:2m