Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
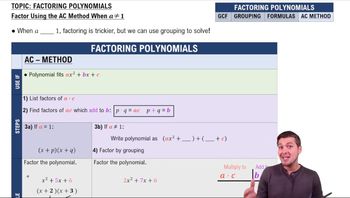
Factoring Polynomials
Problem 96a
Textbook Question
In Exercises 93–100, factor completely. x² − 6/25 + 1/5 x
 Verified step by step guidance
Verified step by step guidance1
Step 1: Begin by rewriting the expression in a standard quadratic form: \( x^2 + \frac{1}{5}x - \frac{6}{25} \).
Step 2: Identify the coefficients: \( a = 1 \), \( b = \frac{1}{5} \), and \( c = -\frac{6}{25} \).
Step 3: Use the method of factoring by grouping or the quadratic formula to find the roots of the equation.
Step 4: If using factoring by grouping, find two numbers that multiply to \( a \times c = 1 \times -\frac{6}{25} = -\frac{6}{25} \) and add to \( b = \frac{1}{5} \).
Step 5: Rewrite the middle term using the two numbers found in Step 4, and factor by grouping to express the quadratic as a product of two binomials.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Factoring Quadratic Expressions
Factoring quadratic expressions involves rewriting them as a product of two binomials. This process is essential for simplifying expressions and solving equations. The standard form of a quadratic is ax² + bx + c, and the goal is to express it in the form (px + q)(rx + s). Recognizing patterns, such as perfect squares or the difference of squares, can aid in this process.
Recommended video:

Solving Quadratic Equations by Factoring
Common Denominators
In the given expression, the terms involve fractions, which require a common denominator for simplification. A common denominator allows us to combine or manipulate fractions effectively. In this case, the denominators are 25 and 5, and finding a common denominator helps in rewriting the expression in a more manageable form, facilitating the factoring process.
Recommended video:
Guided course

Rationalizing Denominators
Completing the Square
Completing the square is a method used to transform a quadratic expression into a perfect square trinomial. This technique is particularly useful for factoring and solving quadratics. By rearranging the expression and adding/subtracting the necessary constant, we can express it in the form (x - p)² = q, which simplifies the factoring process and aids in finding the roots of the equation.
Recommended video:

Solving Quadratic Equations by Completing the Square

 7:30m
7:30mWatch next
Master Introduction to Factoring Polynomials with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice