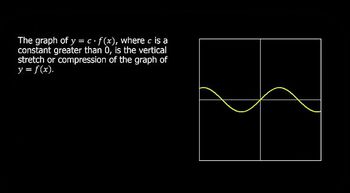
Hi, my name is Rebecca Mueller. During this session, we're going to look at a topic called transformations. Now, in particular, we're going to look at some specific types of transformations you can do on functions in order to change their graphs. We'll look at vertical and horizontal shifts. We'll look at reflections, compressions and stretches, and then combinations of transformations. To begin with, let's review some functions that you should already have at your beck and call. That is, you should be familiar with them, but it's worth the time at the outset to make sure we're familiar with these different functions that we're going to use in this session. Let's start off with f of x equals x squared. Now, this is going to have the shape of a parabola. Its vertex will be at the origin, and we have this symmetry to the y-axis in this format. The other thing to point out is that we have a domain of all real numbers. We have a range from 0 to infinity, including 0, and we can see where it increases and decreases. Another function that we want to be familiar with is f of x equals x cubed, also knows as the cubing function. Notice that we have a section that's in quadrant I and a section that's in quadrant III. And we can see that it increases as we move from left to right. The domain is all real numbers, and so is the range. Let's now look at f of x equals the absolute value of x. This is going to have the distinctive V shape. It's actually two-- you think of it as a linear function that's been separated. The first part that's in the quadrant is the same as y equals x. The part that's in quadrant II is actually if I take my negative xs and now make them positive. As you substitute in to the absolute value, then your y value ends up being positive, also. So again, the distinctive V-shape of the absolute value function. The domain is all real numbers. The range would be all values of y greater than or equal to 0. Then we look at the square root function, which is going to have the equation f of x equals the square root of x. It's going to be a quadrant I function. The domain will be all values of x greater than or equal 0, and the range is all values of y greater than or equal to 0. And so it looks kind of like a parabola-- half of a parabola on its side. So again, these are functions that we want to be familiar with, so that we can use them in order to do some problems. So now that we have some basic graphs that we're familiar with, we're going to use those in order to look at some transformations, and the first transformation we want to consider is a translation, which is going to be a shifting. Let's start off with the following diagram. The graph of y equals f of x plus k is a vertical shift of the graph of y equals f of x. So in my diagram, you'll see that I have drawn a function that is going to be given as f of x. That's y equals f of x. If my value of k is positive-- so if I end up writing, for instance, f of x plus 2 or plus 1, then we're going to shift the graph up k units. So for instance, this whole graph would move upward. If it turns out that the value of k is negative, so that you'd be subtracting at the end of this function, then we're going to shift the graph down k units. You can see that that happens in this diagram. So let's look at an example of where we have to do this by hand. So I'm going to look at the function f of x equals x cubed plus 2. So notice that I'm thinking about having an original function, y, which is equal to x cubed, and that should be one of the functions that we're familiar with. So let's just quickly sketch that in. So drawing in an xy plane. Remember that the x cubed function-- we can plot a few points if you'd like. We're going to have-- it goes through the origin. We can plot the 1, 1, and we know that in the first quadrant, it's going to continue upward like this. And in the third quadrant, it's going to continue downward like that. So that's going to be the graph of y equals x cubed. What I want to now graph is f of x equals x cubed plus 2. So we notice that this is in the format where what I'm doing is applying the function-- that is, I'm cubing first-- and then I'm adding 2 at the end. So it's like taking your old y value and then adding 2 to it. So everything is going to be shifted upward 2 units. So for instance, the point that used to be at the origin is now going to be 2 units up. The point that used to be at 1, comma, 1, is now going to end up being at 1, comma, 3. And I'm really not going to plot a lot more points because I just want to see the idea behind it. I'm going to end up connecting the dots and drawing in this same picture, only notice it's been shifted upward 2 units. And so that's the idea, is trying to sketch these graphs in a quick manner, just to see where the translation is going to take them. So we just looked at a problem dealing with vertical shifts. Now, let's look at one that has horizontal shifting going on. We'll look at the generalized version in that the graph of y equals f of x minus h is a horizontal shift of the graph of y equals f of x. So we have pictured here the graph of y equals f of x, which looks like the parabola-- the squaring function. And we're going to note that if our h value is positive, we're going to shift the graph to the right h units. So before I look at the picture of what's going on, let's just again reiterate that the h value in the format is being subtracted. So when you're looking at it, you're going to think of x minus h, and then the h is positive. When that occurs, we end up with a shift of that graph to the right h units. If it turns out that the h value is negative, then we're going to shift the graph left h units. And so instead, we move left. So let's now look at an example of how we're going to use this. The function that I want to consider is f of x equals the square root of x plus 1. So the function that you're familiar with already is the graph of y equals the square root of x. Just recall that this would be the square root function. It's going to have an end point at the origin and it's going to be in the first quadrant. We could plot a couple of points just to make sure you're familiar with it. If I substitute a value of x equals 1, we come up with square root of 1, which is 1. If I substitute in the value of x equals 4, we can take the square root of 4 in order to end up with the value, 2. And then recall this is the one that kind of looks like a parabola on its side, only you only get half of it. So connecting the dots, here's a diagram of that y equals the square root of x. So the function that I'm looking at now has the square root of x plus 1. Notice that the addition of 1 is directly to the x value. It's not going to happen after the square root has taken place. It happens previous to that. So that's important to our thought process. If I rewrite this, instead of just writing it as the square root of x plus 1, let's rewrite it as the square root of x minus-- because remember in the formula, it's x minus h. What would I be subtracting? I'd have to change the sign and end up with negative 1, so that my h value is going to equal negative 1, which means that the value is negative, and when that occurs, we end up with a shift to the left of 1 unit. So I'm going to take my picture that I have here and I'm going to shift those three points the left 1 unit. So the point that used to be at the origin, moving left, ends up being at negative 1. The point that used to be at 1, comma, 1 shifts left and ends up at 0, comma, 1. The point that used to be at 4, comma, is now going to shift to 3, comma, 2. And I'm going to draw in the same picture. That's going to be that parabola on its side, going off in this direction. But notice that it's all been shifted to the left one unit. Now, I want to reinforce a couple of things here, in that if you look at this picture and you think about its domain, the domain of the graph, according to my diagram, should be all values of x, such that x is greater than or equal to negative because I can see I go from negative to positive infinity. Well, if I look back at the functional format, which is the square root of x plus 1, we know that underneath a square root, the radicand-- the x plus 1-- cannot be negative. That is, x plus 1 has to be greater than or equal to for this square root to be defined in the set of real numbers. Solving this inequality gives us x is greater than or equal to negative 1, and that, of course, corresponds to what we saw graphically. So it's always a good idea to use other information that you know about functions and about expressions to make sure that you're on the right track when you're doing these transformations. So now that we've seen a few things about translations, let's look at the following problem. We want to graph f of x equals x minus 2, quantity squared, minus 4. So first of all, let's recognize the basic graph that we're looking at has the equation y equals x squared. And just quickly, let's put that into our graph here. We know that this is the parabola that has the vertex at the origin, and just putting a couple of more points down for reference, we're going to draw that in the first quadrant and into the second quadrant. There. So we have a parabola drawn. Now, what we notice is that in the function, f of x, all we're doing is adding or subtracting constants. That's key here. When you add or subtract a constant, that ends up being a vertical or horizontal shift. So we have to recognize which is going on with the numbers and the number 4. So we have a subtraction of 2. So let's just think about the fact that if we have f of x equals-- and I'm going to go ahead and use the format with it squared-- and I've got x minus h, that's the format. And then the plus k comes on the end. Then what we have is a horizontal shift because we have the subtraction of 2 in our problem applying directly to our x value. So remember, xs tell you how to move horizontally, so when you are going to affect the x value directly, it makes sense that what you get is a horizontal shift. In our case, f of x is equal to x minus 2, quantity squared, and then we have a plus negative 4. I'm just rewriting it so that we can see exactly what the h and the k are going to be here. This value of 2 is going to be a horizontal shift, and because of the fact that the h value in this format is positive-- that is, we're subtracting a positive 2-- this is going to be a shift to the right of 2 units. Now at the end, we have an addition of k. That is, we already square, so if this is our squaring function that we're applying this transformation to, we have already squared, and then afterwards, we add a negative 4. So what that means is that we're going to have this negative 4, indicating a vertical shift. And because the value is negative-- we're adding a negative 4, which is the same as subtracting 4-- this is going to be a movement down, and we're going to have a movement down of 4 units. So if we go to our diagram now, we can see that the point that was at the origin-- that was the vertex of the parabola-- has to move 2 units to the right, and then 4 units down. 1, 2, 3, 4. It ends up being positioned at the point whose coordinates would be 2, comma, negative 4. Now, we know it's a parabola that's going to open upward. It's going to have the same shape. You know, it's always a good idea when it's easy enough to do to plot a couple of more points, just to make sure you're in the right area. As we go upward, we notice we're going to end up having some x-intercepts. So for instance, it's very easy to find the y-intercept in this function. If I evaluate f of 0, we're going to end up having 0 minus 2, which is negative 2. We square it to give us 4, and then 4 minus is going to end up giving us 0. So f of 0 is going to equal 0, which means that we're going to end up having this point at the origin as another point on our new graph. So as I'm heading upward to the left-- oops. I can see I want to make sure I go through the origin. Play like that's straight or straighter. Well now, let's just think about the fact that because we have the symmetry, that means we've moved 2 units to the left to end up at this intercept, we're going to end up moving to the right to also end up at an intercept. So that means right here at the value of 4, we're also going to have an x-intercept. We can double check that by substituting into the function. We find f of 4. We're going to end up having 4 minus 2, which is 2. 2 squared is going to be 4. And again, 4 minus 4 is going to give us 0. So f of 4 is 0. If I get another x-intercept here, and again, let me kind of stand in front to draw it in. Here, we have our new parabola. So we end up being able to shift this parabola over 2 units to the right and 4 units down, and come up with its graph fairly easily. So again, I just did the extra steps of finding the intercepts because it was pretty easy to do, and I might as well be as accurate as possible while I'm graphing. It's time for a quick quiz. What translations of the graph of f of x equals x cubed can be implemented in order to graph g of x equals 2 plus the quantity x plus 15 cubed? Should we translate Up 2 units, and Right 15 units that's A. B. Left 2 units, Up 15 units or C. Left 15 units, Up 2 units. Choose now from A, B, or C. You're right the answer is C. The translation will be Left 15 units, Up 2 units. Sorry the correct answer is C. The translation should be Left 15 units, Up 2 units. When working with shifts we can think about coming up with format y equals a function f of x minus h where the value of h would be a horizontal shift plus k where the value of K would be a vertical shift. In our equation I'm going to re-write g of x in the other order will have g of x equals now the f of x function is x cubed so we're going to have the quantity x plus which I can write is x minus a negative 15 quantity which is going to be cubed plus the value of 2. So we can see that in this format. Our h value is going to equal negative 15. Our k value is going to equal positive and when we can identify the h value as a negative number it means a shift to the left. So that's going to be a shift left of 15 units. Our k value is a positive 2 and that means we're moving up 2 units. So the graph of the g of x can be found by translating the graph of f of x Left 15 units and Up 2 units. Now we're going to move on to our second type of transformation that we're going to consider, and that's going to be reflections. So we're going to be able to reflect across the x-axis and across the y-axis. In each case, we're going to be using a negative sign to accomplish that, but it depends on where the negative side is applied as to what type of reflection you end up with. Here's the first one. The graph of y equals negative f of x is a reflection of the graph of y equals f of x across the x-axis. And so we end up with the reflection, where it's just flipped over the x-axis. Notice that in this case, we're ending up applying the negative sign after the function has taken place. So notice it does not apply to x directly. It applies to f of x, which is why it makes sense that it reflects to where we take a y value and change it to a negative y value. So here's an example we want to use in order to demonstrate this by hand. Let's look at the function, f of x equals negative the absolute value of x. Now, the function that is our basic format has the equation, y equals absolute value, x. And we may recall that if we do a quick sketch-- so just draw xy plane-- that the graph of y equals the absolute value of x has the distinctive V shape, where it's in the first and the second quadrant and it splits the first quadrant right in half and it splits the second quadrant right in half. So this is our graph of y equals the absolute value of x. Now that we've put a negative sign in front of it, what that means is we're going to take this graph and we're going to reflect it across the x-axis. That is, we're going to take all of our y values and make them negative. So we end up with a simple flip of this reflection to where we are in, now, quadrants III and IV. And so we end up with our f of x equals the negative absolute value of x in quadrants III and IV, whereas the simple absolute value of x is in quadrants I and II. So now we're going to look at our second type of reflection. The graph of y equals f of negative x is a reflection of the graph of y equals f of x across the y-axis. So what we can see is our diagram has a graph drawn. We're now going to think about the reflection across the y-axis, which takes whatever was in quadrant I and puts it into quadrant II. If there was something in quadrant IV, it would go into quadrant III. So now, let's try one by hand. And what I'm going to consider is the function, f of x equals the square root of negative x. Now, the function that we'd have as our basic graph is going to be the y equals square root of x. And we know what that looks like. If I draw a quick sketch of this-- let's do the x-axes here. Then if I'm going to draw in the square root of x, we know that I have the origin-- just plot just a couple of points to get me going, and I know that it looks like this. I want to now notice that in the function that I'm given, we have a negative sign placed in front of the value of x. Just to reinforce a few things, notice that we know that negative x, which is the radicand, has to be greater than or equal to 0 in order for this function to be defined. Solving that inequality requires me to divide both sides of this inequality by negative 1. Dividing by negative 1 on the left leaves me with x. Division by a negative number requires me to switch the inequality symbol to face the opposite direction, so I end up with x less than or equal to, and then 0 divided by negative 1 is 0, so that what occurs is that the domain of this function has to be the set of all x, such that x is less than or equal to 0. Because of the negative sign in front of the x, that is going to give us the reflection across the y-axis, so that in my diagram, I'm going to end up taking that square root function, and it's going to end up being in quadrant II instead of being in quadrant I, as its original version was. So again, this is my f of x equals the square root of negative x. One more thing, just to reinforce. Notice that the negative sign is applied directly to the x prior to doing the square root function. Let's take a look at another problem with reflections. The function I want to consider is f of x equals-- and I'm going to have it in parentheses-- negative x, and then squared. So we think about the original function, which would have been y equals x squared. I can quickly sketch a graph of that function. It's going to be the parabola with the vertex at the origin. So I'm not going to spend time plotting points here. I just want to get an idea of what's going on. So there's our graph of y equals x squared. Now, according to what we just learned about reflections, when we have a negative sign in front of the x, that means that what we're going to do is reflect across the y-axis. So we're still going to have the squaring function, but we're going to take a reflection of this graph across the y-axis to end up with our resultant function. Well, if we take this and we take this parabola, and we think about reflecting it across the y-axis, notice that because it has a symmetry to the y-axis, what we end up with is exactly the same graph. I'm going to come in here and just kind of go right on top of it because my graph that I end up with is going to be exactly the same. Now, it's hard to illustrate that I've had a reflection going on, but let's just think about this algebraically. When we square a negative x, that means we take negative x and multiply it times negative x. And so a negative times a negative is going to be the positive value. So this expression, algebraically, is equal to x squared. So even though the reflection is taking place, notice that the graph that is the result is exactly the same graph we started with. And this can happen with a number of functions. So it's not a bad idea to think about it algebraically before you end up having to graph it. Now, let's look at another type of transformation. It's going to have to do with multiplying or dividing by a constant value, and so let's look at a diagram of what can occur. The graph of y equals c times f of x, where c is a constant greater than 0, is the vertical stretch or compression of the graph of y equals f of x. So we have pictured here a graph that we're going to say is y equals f of x. If the C value is greater than 1, we'll stretch the graph away from the x-axis so that what occurs is we have this situation where we end up having what we're going to call a stretch. Going back to our original, if our value of c is between 0 and 1, we're going to compress the graph closer to the x-axis. So that would look something like this. So notice in these instances, we were multiplying by c, and after we had already applied the function. Now it's easier to see what's going on really when we're going to draw them ourselves, so let's try to demonstrate that now. We're going to have first of all, let's consider the graph of f of x equals two times x squared. So in this case what we have is a value of c that's being multiplied after the function has already taken place. That is we're looking at the squaring function as our basic graph. So let's consider our y equals x squared and we know that this is going to be a parabola with its vertex at the origin. So again, let's kind of do a quick sketch right now drawing some axes. And if I plot the vertex here and I'm going to have a one, one and a two four then I can draw in my graph of y equals x squared using the symmetry of the y axis. So here's my y equals x squared. Now what's going to occur here is I'm multiplying by two and remember that this is going to have this kind of effect of. Look at my hands, I'm going to be pulling it away from the x axis. It's going to be a stretch. Whenever you have the multiplication by c after the function has occurred, you're going to have either a pulling away or a compressing toward. In this case, my value of C is greater than one, so that's going to be the stretching that's going on. If I just plot a couple of points, we'll see what, how that impacts my graph. Again, plugging in a zero for x into my function, f of x gives me back the origin, but when I plug in the value of one here, I'm going to square it and then multiply by two. So when x is one, I end up getting the value of two. So what you can see just by those two dots just to give me an idea as I still get a parabolic shape, so I want to draw this in as a parabola, but it's going to go now it's going to be stretched upward and notice that it's been pulled them away from my x axis. So again, think of it by doing this. Let's nail in the same graph. Let's consider the function f of x equals as called g of x actually, let's look at g of x and we're going to make that equal one half x squared. So now I'm still multiplying by a value of C. It's being multiplied after the function has already taken place that is already squared, and now I'm going to multiply by one half, but this is going to be the second case that we saw, in that we're going to multiply it by a number between zero and one. If we plot a point or two, you'll see the idea. Let's let x equals zero in this, we're going to end up with a value of zero. So I still have the origin, this new graph, if I allow x to equal one, we're going to have one squared, which is one times one half. So at one I'm down here at one half. It's still going to look like that parabolic shape, but notice it's going to have been compressed, to where it's going to be closer to the x axis. So again, think about your parabolas is (inaudible) was a actual physical thing in where multiplication by two, we're going to pull it up this way. In the multiplication by one half, we're going to flatten it out like this. So that we end up with that graph that looks wider than it was before. Another way to describe this is that the multiplication by two was going to narrow the graph and the multiplication by one half was going to widen the graph. Now we're going to look at another case where we're going to multiply by constant, but this time it's going to be in a different location as far as where the function is concerned. So let's consider that next. The graph of y equals f of Cx, where C is a constant greater than zero is the horizontal stretch or compression of the graph of y equals f of x. So what we see here is a diagram of a function we'll call y equals f of x. If our value of C is greater than one, we compress the graph toward the y axis in this manner. Back to our original. If our value of C is between zero and one, we stretch the graph away from the y axis. It's time for a quick quiz. Which operation in column A matches to the transformation next to it in column B? So we have a column A to the left and column B to the right. The operation that's given is number one in column A is multiplication by a constant greater than one. The transformation next to it in column B is a shifting of the graph. Number 2 in column A is an operation which is addition of a constant. The transformation next to it in column B is a stretch or compression of the graph. And number 3 in column A, the operation is given as multiplication by the number negative 1. The transformation next to it in column B is a reflection of the graph. Choose 1, 2 or 3 as the operation that is matched up to the transformation that's next to it in column B correctly. You're correct, the operation is matched correctly is number 3, Multiplication by the value negative 1. Sorry the operation that's match correctly from column A to column B is number 3, Multiplication by negative 1. Let's consider each operation and independently if we look at multiplication by a constant greater than one that is going to lead to the transformation which they stretch or compression of the graph. So that's number B or part B in column B. When we look at the second operation is given which is addition of a constant that is going to be associated with the transformation which is a shifting of the graph which is given as number A, as part A in column B. When we look at multiplication by negative 1 which is the answer it is matched up to the transformation which is a reflection of the graph and that's given directly across from it in column B. Now, in this situation, notice that we're multiplying the value of c times x directly, and then applying the function after the fact. So as an example of this, let's consider the function, f of x, which is equal to the value, 2x squared. So this is the situation where we have the multiplication of directly toward the x. Let's see what that's going to look like when we try to graph it. Again, we're going to use as our reference our basic graph of y equals x squared. And we're going to quickly sketch our parabola in, and then see what happens when we have the 2x here. So again, very quickly, let's put in this parabola. And I'll do a couple of points of reference. So if I let x equal 1, then our y value is 1. If I let x equal 2, then our y value is going to end up being 4. I get that nice picture in the first quadrant, and then make it symmetrical in the second quadrant. And there we have our diagram of y equals x squared. Now, what this is supposed to do is that multiplication of the times the x is supposed to be a compression, and we're going to see how that works by plotting a few points. Let's just take x and then our f of x, and let's substitute in a couple of values. If x is equal to 0, we have 2 times 0, which is 0. We square it. We end up with 0. Let's let x equal 1. Now, what's going to happen is we're going to multiply 2 times 1, which is going to give us 2, and we're going to square it and end up with 4. So we have the point, 0, 0, and then we have the point, 1, 4. And now, if I plug-in another value, such as-- let's just do something like 1/2-- we're going to have 2 times 1/2, which is 1. And when we square it, we end up with 1. So at 1/2, we end up with the value of 1. And now, it's got to be the parabola or that shape that we're looking at. Notice that it has a slightly different look to it. Now, it's kind of funny because it looks like what we've done is to actually-- what we had previously was like stretching it upward. But what we're thinking about here is that it's actually this effect where we're compressing it toward the y-axis. Well, you can see that really, you can think about it in one of two ways. You can say, oh yeah, that's what happened to the parabola. I pushed it in toward the y-axis. I could also think about it as I pulled it away from the x-axis. If I do a little bit of simplification on our f of x, we note that when we square 2x, we square the 2, which gives us a 4, and then we square the x to give us an x squared. So algebraically, it makes sense that we can look at this diagram and think about what happened to the graph in two ways. We can either say that what we did was pull it, stretching it this way-- vertically-- or we can think of it as a compression horizontally. And this is going to occur for a number of the different functions that you're familiar with. For instance, if I look at a y value equal to the absolute value of 5x, then what I can see is that I'm multiplying the 5 times the x, which should make me think of it as a compression in toward the y-axis. But you know, if I do a little bit of algebra on this, this is the absolute value of 5 multiplied times the absolute value of x, and that's 5 times the absolute value of x. Now, I'm performing the function first, and then I'm multiplying by 5. And so that makes me think of a stretch in a vertical direction. Likewise, if I had a g of x, which is equal to the square root of 2x, I can see this as a multiplication by 2 times x or I can take the square root of and multiply it times the square root of x, which is equivalent, and see it as a multiplication by square root of after I perform the function. So when you're dealing with these examples, try to see if you can simplify or you can think of it as a compression the other way. As a student, you should be able to apply any of these transformations to a known graph, and the key here is knowing the order in which to do the applications. So let's consider the ordering of our transformations. We're going to use the following rule of thumb. That is, that we're going to first do stretches or compressions. Now, recall that we end up with a stretch or a compression when we multiply by a constant value. So if you think about order of operations, you do multiplication before you do addition or subtraction. And so that's going to make a little bit of sense here. The other thing is the second one is going to be reflections. Those reflections are accomplished by having negatives. So think about it as multiplying by a constant to get our stretches or compressions, and then we apply the negative sign afterwards to get our reflections. Finally, the shifts, which are going to be occurring whenever we're adding or subtracting a number, are going to be the things that we're going to apply last. So this is important because you can end up with a different graph if you shift up or down, for instance, and then reflect, as opposed to reflecting and then shifting up or down. Let's look at an example to see how we're going to apply this. So let's look at the function, f of x equals-- and what I'm going to do is have a negative 1/3 multiplied times the absolute value of x minus 4, and then we're going to add 1 at the end. So one thing we want to do is be able to identify what the different transformations are that are going on. Our basic function is going to be the graph of y equals the absolute value of x, which you'll recall is going to be the V-shaped graph. Let's just now point out some of the things that we see occurring by the format of this expression. Well, we notice here that we have a minus 4, so we start off with the x, and then we subtract the 4. And that's going to be a horizontal shift. Because our original format is x minus h, when we're thinking about horizontal shifts, the h value here is going to be a positive 4. So this 4 right here is going to tell us that we're going to take this graph and we're going to shift it to the right 4 units. We then notice that we have a multiplication by 1/4, and so that multiplication by one third, which you notice is occurring after you've taken the absolute value-- and also note that I'm separating the negative sign from it on purpose here. I just want to think about the 1/3-- that multiplication. That's going to end up affecting this, and we're going to think about it in the vertical way. So in this case, because the 1/3 is between 0 and 1, we're going to end up having that graph being compressed toward the x-axis. So this is again going to be a compression, and we're going to compress it toward the x-axis. Now, let's consider what the negative sign is going to do. That negative sign is again applied not directly to the x, but it's applied to the functional value, If you about it as being applied to the absolute value. So that is going to end up being a reflection, but this is going to be a reflection across the x-axis. So we going have that reflection cross the x-axis. And then we have the plus 1 at the end, and again, this is being applied not directly to the x, but it's being applied to the f of x if you want to think of it like that, to the functional value. And so in the original format where we learned our rules, this is going to be like a k value that's happening at the end. This is going to be a shift in a vertical direction. Because the value of k is positive, that's going to be a shift upward of 1 unit. So this 1 right here is going to tell us to shift it up 1 unit. So we have four different transformations that are going to take place. In order to graph the function, we want to think about the order in which we're going to apply these. And again, using the idea of how we work with numbers, we think about multiplication, and then we can think about the negative being played into the part. And then we're going to have the addition at the end. So to order these, the first thing that we want to do is going to be impacted by the multiplication by 1/3. So the first thing that's going to happen is going to be the compression, and that compression is going to be toward the x-axis. The second thing that's going to occur is going to be the reflection. That's going to be the minus sign-- the negative that takes place. So then we're going to have the reflection that takes place. And then the last thing that will occur will be the shifting. And the shifts can occur in either order. We can either shift to the right first and then up, or vice versa. But I'm going to go ahead and just say that we'll shift to the right those 4 units, and then finally, I will end up shifting upward 1 unit. So this is what I want to do to the graph of y equals the absolute value of x. So again, let's just do a quick sketch here. And remember that if I look at y equals absolute value of x, that I'm looking at this V-shaped graph. So according to this, we're going to do, first, a compression toward the x-axis. Now, I probably need to plot some points in order to get it in an accurate manner, so let's try to do that now. If I just plot, I think, one more point, I'm going to get an idea of what should be happening here. So when I think about this compression toward the x-axis, it's going to be 1/3 of what it was before. So if this is a value of 1, then I'm now going to end up at 1/3. So it's going to be pulling it down toward there. So if I just look at that, what's going to happen is this kind of a shape. OK? So then, what we'll do is we'll have a reflection. So I'm going to reflect that now across the x-axis, and that's going to end up taking this picture, and instead of being in quadrants I and II, it's going to be in quadrants III and IV. So I'm take my compressed version, kind of draw it in, and then what will happen? Well, now we're going to end up shifting it to the right 4, and then we're going to shift up 1. So I can shift to the right 4 units. Let's just go 1, 2, 3, 4. And I'm going to go ahead and do these two together, and then shift up 1. So this is my graph that I have right now. Move it over to the right and then up 1, and I'm going to end up having this picture coming in where I know I'm going to end up having it upside down. Now, I'm not going to plot any more points right now, so I'm not guaranteed that I'm going to have it at the correct values on the x-axis. But I'm just going to kind of do this just to get the general idea. So this last version is going to be really the idea of what I want to end up with. So I've drawn a lot of intermediate steps. Now, if I'm doing this in practice, I may not want to draw four different graphs. I may just want to list what I'm doing, get an idea of what my final result should look like, and then give myself some points of reference. Now, you may think to yourself, you know what? If I'm going to be having to have this plotting of points anyway, then what's the purpose of knowing all of the transformations? Well, remember that what you're finding out is that you know what that graph looks like. Just because you know what the basic graph looks like, you know it's going to have this V shape because you understand that all that's going on are some transformations. So I know that I can take, for instance, if I want to cut to the chase instead of drawing all the intermediate steps, I can take the point that used to be at the origin and think about what would happen. When I compress it, it doesn't move. When I reflect it, it doesn't move. I'm going to shift it to the right 4 and up 1. So that point of the V that used to be at the origin is now going to be at the point, 4, comma, 1. And I know it's a V shape that's been reflected over. You know, another good thing to always determine are going to be your intercepts, and your y-intercept is an easy one to find. So I'm going to find f of 0 by substituting into my function. That's going to give me a negative 1/ times the absolute value of negative 4 plus 1. So that's going to be a negative 1/3 times 4, which is going to be negative 4/3, plus 1, which is 3/3, and so I end up with a negative 1/3. So I know that over here on the y-axis, here I am right here. You could also find your x-intercepts, and you can do that by setting this function equal to 0. So let's go ahead and do that now. If I have negative 1/3 times the absolute value of x minus 4 plus 1 equals 0, I can subtract from both sides of the equation. So negative 1/3 times the absolute value of x minus equals negative 1. I'm going to multiply both sides of that equation by negative 3. So that's going to give me the absolute value of x minus equals a value of 3, and then really, by inspection, you can see that if I want to end up with a 3, I can either make x minus 4 equal positive or I can have x minus 4 equal to negative 3. That's going to give me x equals 7 for the first equation and x equals positive 1 for the second equation. So I can see that on my graph, if I plot my x-intercepts-- this is at 7-- that I get some more points of reference. And I end up with the graph that is the resultant. You can see that instead of doing all the intermediate steps, I can go directly to the graph that I'm looking at. And so I put a lot more into this than you had to in order to get to this graph, but I wanted to demonstrate a number of different methods for coming up with an accurate graph at the very end. Next, we're going to look at an example where we're going to look at things in the opposite order than what we've been looking at. Here's the problem I want to work with. Write an equation of the function whose graph fits the following description. The graph of y equals x cubed is going to be shifted left 2 units, then reflected about the x-axis, and then shifted down 5 units. So the idea is we've got a description of a graph. We want to come up with an equation for that function. So the graph is going to be the basic graph of y equals x squared. Let's take each thing individually. So the first thing is we see that we're supposed to shift it. And it's supposed to be shifted left 2 units. So how can we write that? Well, we know that we're going to be dealing with f of x, and our basic function would have been f of x equals x cubed. If we're going to shift it to the left 2 units, that means we're going to have to add or subtract directly to the x value. To make it move to the left, we need to think about moving it 2 units-- think about it in the negative direction. So that subtracting a negative 2, or I can write it down symbolically as x plus 2. That's going to be a shift to the left, and then of course, we've got the cubing that's going on. So the first part of it-- shifting left 2 units-- is going to be f of x equals the quantity, x plus 2, cubed. And then let's go to the next thing. We then want to reflect it about the x-axis. So we want to reflect about the x-axis. And to accomplish that, we know that the reflection is going to have a negative sign involved. Now, if we put the negative sign directly on the x, that's when we flip it across the y-axis. So to reflect it across the x-axis, what we need to do is have the negative sign occurring after the function has taken place. In other words, after the cubing. So I'm going to just go ahead and keep calling it f of x. We're going to have f of x equals-- we're going to have the negative now out front, and then we're going to have the x plus 2, quantity cubed. And now we're then supposed to shift it down 5 units. So to shift down or any vertical movement, we're going to have to apply this after we have performed the function, which means to go down, we're going to subtract a value of and we're going to do it at the tail end of this function, f of x. So I'll go ahead and again just keep calling it f of x equals-- we're going to take what we had before-- the negative x plus 2, quantity cubed, and we're going to now put a minus on the end. So our final result is going to occur when we've performed all of the steps. In our next example, we're going to look at working with a function that you're not necessarily familiar with. In our picture, we have a diagram where we're going have a function that we're going to call f of x. We're then going to attempt to graph the value where we have a new function, y equals the negative of f of 2x minus 4 minus 1. So we'll get back to actually taking it and ending up with the points that we're going to work with, but let's just work with this for a second. One thing to note is that inside the parentheses, we see the 2 times x minus 4. Now, what we're accustomed to working with is where we have the x being affected directly by numbers. And so we can see the multiplication by 2, but you see this minus 4? That minus 4 is taking place after you've multiplied by 2. So I'm going to rewrite this a little bit. I'm going to say this is actually equivalent to y equals negative f of-- and now I'm going a write the 2 times x minus 2, in parentheses, minus 1. What that means is I can see that that subtraction of is affecting the x directly, and so that's going to end up being a horizontal shift. So we're now going to look at what we just determined, and we're going to put it in the order in which it needs to be applied. So remember, we're going to do compressions first, and therefore, we're going to think about this as a compression horizontally by a factor of 2. And then next, we know that we would be doing any kind of reflections. And so this reflection is going to be across the x-axis. And so let's list this. Then we have two shifts. We have a shift to the right of 2 units, and then we have a shift downward of 1 unit. So let's list that. Shift right 2 units, and then we have the shift downward of 1 unit. Now, I've listed them in this order because I want to concern myself with what happens to each of the endpoints of these three line segments. We can determine that we have, to begin with, the point that is located at negative 4, comma, 2. So I'm going to list that here. And then that is connected via line segment to the point, whose coordinates are 0, comma, 3. We then connect that to the point, 2, comma, negative 2. And then that is connected to the point, 5, comma, 4. Now, what I want to do is consider how each of these different transformations will affect each of those points. So let's begin with a compression horizontally by a factor of 2. Now, what that means is that we start out here at the point that used to be at negative 4, comma, 2, and we're going to compress horizontally. So that's going to end up bringing it inward, and notice that if I use a factor of 2, then this point is now going to be at the location, which is negative 2, comma 2. That is, we're going to divide by 2, and that's the x-coordinate because of the compression horizontally. So using that same idea, we divide the x-coordinate by 2. That gets us to the point, 0, comma, because division by 2 when we're working with the number is still 0. 2 divided by 2 is going to be a 1, and that y-coordinate remains the same. 5 divided by 2 is going to be 5/2, and the y-coordinate remains the same. So what I've done is figure out what happens because of the compression. Now we're going to reflect across the x-axis. What does that do to a particular point? Well, if I start with a point that's 2 units above the x-axis, as in this case, and I reflect it across the x-axis. That means it ends up giving me a negative value for that y that's given in the original point. In other words, this point is now going to be located at negative 2, comma, negative 2. The next point would be 0, comma, negative 3. Then we're going to have the point, 1, comma, 2. And then the point, 5/2, comma, negative 4. Again, reflecting across the x-axis takes the y-coordinate and switches its sign. Let's shift to the right 2 units. Which coordinate will that impact? Well, movement right or left is always going to be an x value, so we're going to end up shifting to the right 2 units, which means I'm going to have an addition of 2 units to the value of x for each of these points. So let's take the first point, add 2 to our x-coordinate, and we end up at 0, negative 2. For our second point, add 2 to the x-coordinate. It's going to be at 2, negative 3. Add 2 to 1 to end up at 3, comma, 2. Add 2 to 5/2. Well, that's the same as adding 4/2 to 5/2. So that's going to be 9/2. And then the y-coordinate remains the same. And finally, we want to shift down 1 unit. Now, that's going to impact our y-coordinate of our points because shifting down is going to be a vertical movement. So I'm going to subtract 1 from each of the y-coordinates on these points. The first point, if I subtract 1 from negative 2, that will end up giving us negative 3. So the x-coordinate remains the same, but the y coordinate is going to switch. We're going to subtract 1 from negative 3, so this second point becomes 2, comma, negative 4. We're going to subtract 1 from 2, so this next point becomes 3, comma, 1. And we're going to subtract 1 from negative 4, so that's going to be 9/2, comma, negative 5. This last column is what I'm interested in, as far as getting back to the graph over here. I'm going to take those four points and I'm going to now plot them on our graph. So we're going to have the point, 0, negative 3. So I'm going to go down three units on the y-axis and plot that point. Then we're going to have the point, 2, comma, negative 4. So at 2, I go down to negative 4 and right here. Now, what's important is this was what occurred when I ended up taking this first line segment and doing all those transformations. So I know that in my resultant graph, this is going to be a line segment. Let's go to the next point, 3, comma, 1. So let's plot it. This is what happened to that middle line segment. I'm going to end up going upward and connecting the dots. And then my last point, which is at 9/2, which is the same as 4 and 1/2-- negative 5. We're going to go to 9/2, and then negative 5, which is about right here. And I'm going to connect that with a line segment, and this is going to be the result of what occurred to the last point that we were working with. So notice I still end up with three line segments, but I've been able to keep track of all the transformations by using this chart, and therefore come up with a new result. Now, one thing to notice is because of the horizontal compression, if we look at the original, it went from negative 4 to positive 5. That's a width of 9 units. When we look at what we end up with here, it goes from 0, which is here, to 9/2. That's taking that 9 units and compressing it by a factor of 2. It turns out that each of these little line segments has been compressed by a factor of 2. And so if you kind of look at each of those little ranges, you'll see that impact on the graph. So this is a method for keeping track of everything, and it's probably the best method for trying to work with something that is-- what can be fairly complicated, but now, it's very structured. So it's time now for you to try some more problems dealing with all of the different transformations. Good luck in your work.
Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 31m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Transformations
Video duration:
5mPlay a video:
Related Videos
Related Practice