Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
1. Equations & Inequalities
Linear Inequalities
Problem 71c
Textbook Question
In Exercises 71–72, use the graph of the polynomial function to solve each inequality. 
2x^3 + 11x^2 ≥ 7x + 6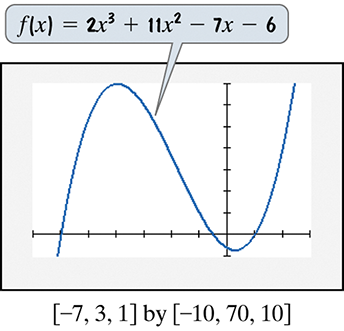
 Verified step by step guidance
Verified step by step guidance1
Step 1: Rewrite the inequality 2x^3 + 11x^2 ≥ 7x + 6 in standard form by moving all terms to one side: 2x^3 + 11x^2 - 7x - 6 ≥ 0.
Step 2: Identify the polynomial function f(x) = 2x^3 + 11x^2 - 7x - 6 and analyze its graph to find the x-intercepts (roots).
Step 3: From the graph, observe the x-intercepts, which are the points where the graph crosses the x-axis. These points are the solutions to the equation 2x^3 + 11x^2 - 7x - 6 = 0.
Step 4: Determine the intervals on the x-axis where the polynomial is greater than or equal to zero by analyzing the behavior of the graph around the x-intercepts.
Step 5: Combine the intervals where the polynomial is non-negative to form the solution set for the inequality 2x^3 + 11x^2 - 7x - 6 ≥ 0.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Related Videos
Related Practice