Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
5. Rational Functions
Graphing Rational Functions
Problem 108
Textbook Question
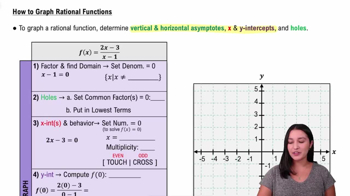
Find a rational function ƒ having a graph with the given features. x-intercepts: (1, 0) and (3, 0) y-intercept: none vertical asymptotes: x=0 and x=2 horizontal asymptote: y=1
 Verified step by step guidance
Verified step by step guidance1
Identify the x-intercepts and vertical asymptotes to determine the numerator and denominator of the rational function. The x-intercepts at (1, 0) and (3, 0) suggest that the numerator should have factors (x-1) and (x-3).
Since there are vertical asymptotes at x=0 and x=2, the denominator should include factors x and (x-2). This gives the denominator as x(x-2).
Combine the factors identified for the numerator and the denominator to form the rational function. The function so far is f(x) = \frac{(x-1)(x-3)}{x(x-2)}.
To address the horizontal asymptote at y=1, ensure the degrees of the numerator and denominator are the same. Since both the numerator and denominator are degree 2, multiply the numerator by a constant to adjust the leading coefficients. Set the leading coefficient of the numerator to match the denominator, which is 1, so the function remains as f(x) = \frac{(x-1)(x-3)}{x(x-2)}.
Verify that the function has no y-intercept, which is consistent with the function since plugging x=0 into the function is undefined, confirming there is no y-intercept.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
8mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rational Functions
A rational function is a function represented by the ratio of two polynomials. It is typically expressed in the form f(x) = P(x)/Q(x), where P(x) and Q(x) are polynomials. Understanding the structure of rational functions is essential for analyzing their behavior, including intercepts, asymptotes, and overall graph shape.
Recommended video:

Intro to Rational Functions
Asymptotes
Asymptotes are lines that a graph approaches but never touches. Vertical asymptotes occur where the function is undefined, typically at values that make the denominator zero. Horizontal asymptotes indicate the behavior of the function as x approaches infinity, providing insight into the function's end behavior and long-term trends.
Recommended video:

Introduction to Asymptotes
Intercepts
Intercepts are points where a graph crosses the axes. The x-intercepts occur where the function equals zero, indicating the roots of the polynomial in the numerator. The y-intercept is found by evaluating the function at x=0. Understanding intercepts is crucial for sketching the graph and identifying key features of the rational function.
Recommended video:
Guided course

Graphing Intercepts

 5:31m
5:31mWatch next
Master Graphing Rational Functions Using Transformations with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice