Here are the essential concepts you must grasp in order to answer the question correctly.
Function Transformation
Function transformation refers to the process of altering the graph of a function through various operations, such as vertical or horizontal shifts, stretches, or reflections. In this case, the function g(x) = ½ f(x) represents a vertical compression of the original function f(x) by a factor of ½, meaning that all y-values of f(x) are halved.
Recommended video:
Domain & Range of Transformed Functions
Graphing Functions
Graphing functions involves plotting points on a coordinate plane to visually represent the relationship between the input (x) and output (y) values of a function. Understanding how to read and interpret the graph of f(x) is essential for accurately graphing g(x), as it allows one to apply the transformation rules effectively.
Recommended video:
Graphs of Logarithmic Functions
Key Points on a Graph
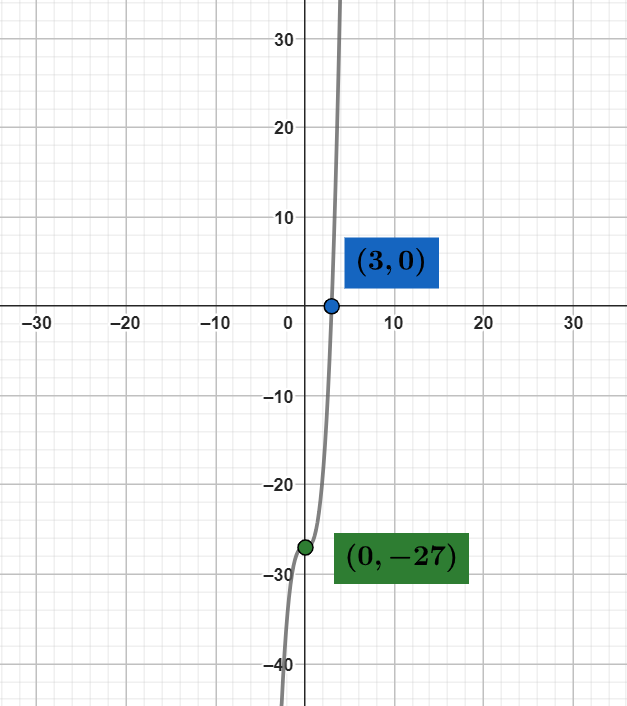
Key points on a graph, such as intercepts and turning points, are critical for understanding the behavior of a function. In the provided graph, the points (3, 0) and (0, -27) are significant as they indicate where the function intersects the axes. These points will also be transformed when graphing g(x), helping to maintain the overall shape of the function while applying the vertical compression.
Recommended video:
Graphing Equations of Two Variables by Plotting Points
 Verified step by step guidance
Verified step by step guidance Verified Solution
Verified Solution



 5:25m
5:25m