Here are the essential concepts you must grasp in order to answer the question correctly.
Rational Functions
A rational function is a function that can be expressed as the quotient of two polynomials. In the given function f(x) = (x^2 - 9)/(x - 3), the numerator is x^2 - 9, which can be factored, and the denominator is x - 3. Understanding the structure of rational functions is essential for analyzing their behavior, including identifying asymptotes and holes.
Recommended video:
Intro to Rational Functions
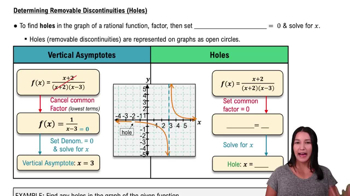
Vertical Asymptotes
Vertical asymptotes occur in rational functions where the denominator equals zero, leading to undefined values. To find vertical asymptotes, we set the denominator of the function to zero and solve for x. In this case, the vertical asymptote is found by solving x - 3 = 0, which indicates where the function approaches infinity.
Recommended video:
Determining Vertical Asymptotes
Holes in the Graph
Holes in the graph of a rational function occur at values of x that make both the numerator and denominator equal to zero, indicating a removable discontinuity. To find holes, we factor both the numerator and denominator and identify common factors. In this function, if x = 3 is a root of both the numerator and denominator, it indicates a hole at that point.
Recommended video:
Determining Removable Discontinuities (Holes)
 Verified step by step guidance
Verified step by step guidance Verified Solution
Verified Solution


 6:24m
6:24m