Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
1. Equations & Inequalities
Linear Inequalities
Problem 84b
Textbook Question
Textbook QuestionSolve each inequality. Give the solution set in interval notation. (x+7)/(2x+1)<0
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Inequalities
Inequalities express a relationship where one side is not equal to the other, often using symbols like <, >, ≤, or ≥. In this context, we are dealing with a rational inequality, which involves a fraction. Understanding how to manipulate and solve inequalities is crucial for finding the values of x that satisfy the given condition.
Recommended video:

Linear Inequalities
Rational Functions
A rational function is a ratio of two polynomials. In the inequality (x+7)/(2x+1)<0, the numerator is x+7 and the denominator is 2x+1. Analyzing the behavior of rational functions involves identifying where the function is positive or negative, which is essential for solving the inequality.
Recommended video:
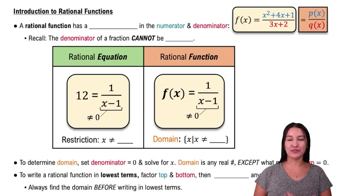
Intro to Rational Functions
Interval Notation
Interval notation is a way of representing a set of numbers between two endpoints. It uses brackets [ ] for inclusive endpoints and parentheses ( ) for exclusive ones. When solving inequalities, expressing the solution set in interval notation provides a clear and concise way to communicate the range of values that satisfy the inequality.
Recommended video:

Interval Notation
Related Videos
Related Practice