Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
1. Equations & Inequalities
Linear Equations
Problem 16b
Textbook Question
Textbook QuestionSolve each problem. (Modeling) Online Retail SalesProjected retail e-commerce sales (in billions of dollars) for the years 2016–2022 can be modeled by the equation y=52.304x+396.80, where x=0 corresponds to 2016, x=1 corresponds to 2017, and so on. Based on this model, find projected retail e-commerce sales in 2022 to the nearest tenth of a billion. (Data from www.statista.com)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Linear Equations
A linear equation is an algebraic expression that represents a straight line when graphed. It typically takes the form y = mx + b, where m is the slope and b is the y-intercept. In this context, the equation y = 52.304x + 396.80 models the relationship between the year and projected sales, allowing us to predict future values based on the linear trend.
Recommended video:

Categorizing Linear Equations
Slope and Intercept
The slope of a linear equation indicates the rate of change of the dependent variable (y) with respect to the independent variable (x). In the given equation, the slope is 52.304, meaning that for each year increase (x), the projected sales increase by approximately 52.304 billion dollars. The y-intercept, 396.80, represents the projected sales when x equals 0, or the year 2016.
Recommended video:
Guided course
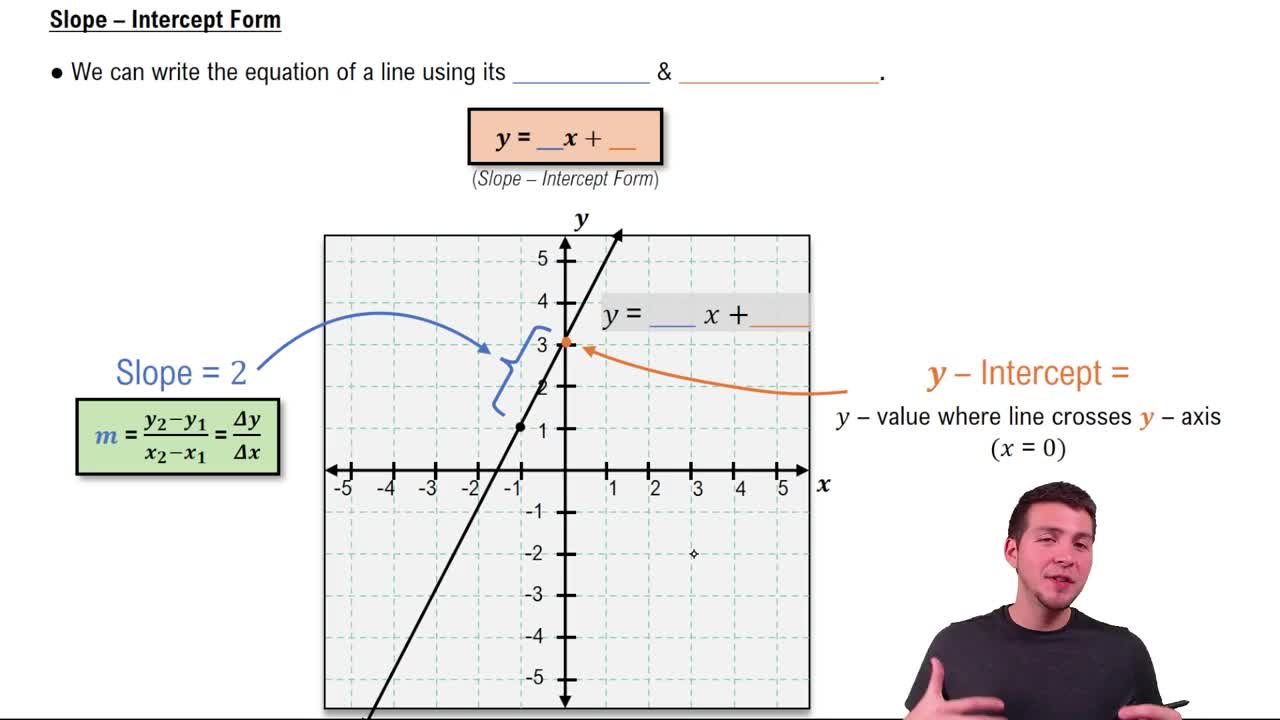
Slope-Intercept Form
Modeling and Predictions
Modeling in mathematics involves creating a representation of a real-world situation using equations. In this case, the equation models online retail sales over a specific period. By substituting the appropriate value of x (which corresponds to the year 2022, or x=6), we can predict the sales for that year, demonstrating how mathematical models can be used for forecasting in business.
Recommended video:

The Number e

 7:48m
7:48mWatch next
Master Introduction to Solving Linear Equtions with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice





