Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
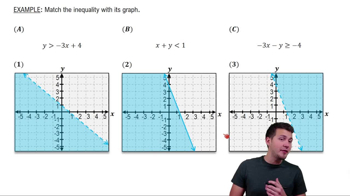
Graphing Systems of Inequalities
Problem 23
Textbook Question
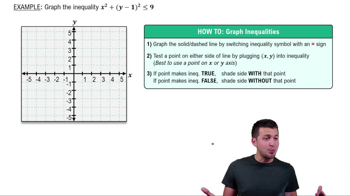
Textbook QuestionGraph each inequality. y > (x - 1)^2 + 2
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
9mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Inequalities
Inequalities express a relationship where one quantity is larger or smaller than another. In this case, the inequality 'y > (x - 1)^2 + 2' indicates that the value of y must be greater than the value of the quadratic expression on the right. Understanding how to interpret and graph inequalities is crucial for visualizing the solution set.
Recommended video:

Linear Inequalities
Quadratic Functions
Quadratic functions are polynomial functions of degree two, typically expressed in the form f(x) = ax^2 + bx + c. The expression '(x - 1)^2 + 2' represents a parabola that opens upwards, with its vertex at the point (1, 2). Recognizing the shape and position of quadratic graphs is essential for accurately graphing inequalities involving them.
Recommended video:

Solving Quadratic Equations Using The Quadratic Formula
Graphing Techniques
Graphing techniques involve plotting points and understanding the behavior of functions on a coordinate plane. For the inequality 'y > (x - 1)^2 + 2', one must first graph the boundary line y = (x - 1)^2 + 2, then shade the region above this curve to represent all points where y exceeds the quadratic expression. Mastery of these techniques is vital for effectively visualizing solutions to inequalities.
Recommended video:
Guided course

Graphs and Coordinates - Example

 7:2m
7:2mWatch next
Master Linear Inequalities with a bite sized video explanation from Patrick Ford
Start learning