Here are the essential concepts you must grasp in order to answer the question correctly.
Transformations of Functions
Transformations of functions involve shifting, reflecting, stretching, or compressing the graph of a parent function. In this case, the parent function is f(x) = 1/x. Understanding how to apply vertical and horizontal shifts, as well as reflections, is crucial for accurately graphing the transformed function g(x) = 1/(x+1) - 2.
Recommended video:
Domain & Range of Transformed Functions
Vertical and Horizontal Shifts
Vertical and horizontal shifts are specific types of transformations that move the graph of a function. A horizontal shift occurs when a constant is added or subtracted from the x-variable, while a vertical shift involves adding or subtracting from the entire function. For g(x), the term (x+1) indicates a horizontal shift left by 1, and the '-2' indicates a vertical shift down by 2.
Recommended video:
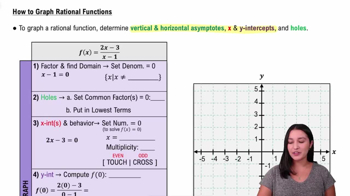
Graphing Rational Functions
Graphing rational functions requires understanding their asymptotic behavior and intercepts. Rational functions can have vertical asymptotes where the denominator equals zero and horizontal asymptotes that describe the end behavior of the function. For g(x), identifying these features will help in sketching the graph accurately, particularly noting the shifts and asymptotes resulting from the transformations applied to the parent function.
Recommended video:
How to Graph Rational Functions
 Verified step by step guidance
Verified step by step guidance Verified Solution
Verified Solution


 6:24m
6:24m