Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
5. Rational Functions
Graphing Rational Functions
Problem 81
Textbook Question
In Exercises 81–88, a. Find the slant asymptote of the graph of each rational function and b. Follow the seven-step strategy and use the slant asymptote to graph each rational function. f(x)=(x^2−1)/x
 Verified step by step guidance
Verified step by step guidance1
<Step 1: Identify the type of asymptote.> Since the degree of the numerator (2) is exactly one more than the degree of the denominator (1), the function has a slant (oblique) asymptote.
<Step 2: Perform polynomial long division.> Divide the numerator \(x^2 - 1\) by the denominator \(x\) to find the slant asymptote. The quotient will give the equation of the slant asymptote.
<Step 3: Set up the division.> Write \(x^2 - 1\) under the division bar and \(x\) outside. Determine how many times \(x\) goes into \(x^2\), which is \(x\).
<Step 4: Multiply and subtract.> Multiply \(x\) by \(x\) to get \(x^2\), subtract \(x^2\) from \(x^2 - 1\) to get \(-1\).
<Step 5: Interpret the result.> The quotient from the division is \(x\) with a remainder of \(-1\). Therefore, the slant asymptote is \(y = x\).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
16mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Slant Asymptote
A slant asymptote, or oblique asymptote, occurs in rational functions when the degree of the numerator is exactly one higher than the degree of the denominator. To find it, perform polynomial long division on the function. The quotient (ignoring the remainder) gives the equation of the slant asymptote, which represents the behavior of the function as x approaches infinity.
Recommended video:

Introduction to Asymptotes
Polynomial Long Division
Polynomial long division is a method used to divide a polynomial by another polynomial of lower degree. It involves dividing the leading term of the numerator by the leading term of the denominator, multiplying the entire denominator by this result, and subtracting it from the numerator. This process is repeated until the degree of the remainder is less than that of the divisor, allowing us to find the slant asymptote.
Recommended video:
Guided course

Introduction to Polynomials
Graphing Rational Functions
Graphing rational functions involves analyzing key features such as intercepts, asymptotes, and end behavior. The seven-step strategy typically includes finding the domain, intercepts, asymptotes, and testing points in intervals to understand the function's behavior. The slant asymptote provides a guide for the function's behavior at extreme values of x, helping to sketch the graph accurately.
Recommended video:
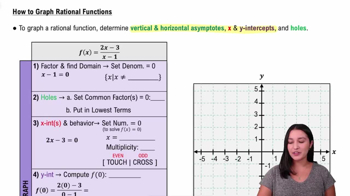
How to Graph Rational Functions

 5:31m
5:31mWatch next
Master Graphing Rational Functions Using Transformations with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice