Here are the essential concepts you must grasp in order to answer the question correctly.
Graphing Constraints
Graphing constraints involves plotting inequalities on a coordinate plane to visualize the feasible region where all constraints are satisfied. Each inequality represents a boundary, and the area where these boundaries overlap indicates the possible solutions. Understanding how to graph these constraints is essential for identifying the region of interest for optimization problems.
Recommended video:
Graphs and Coordinates - Example
Objective Function
An objective function is a mathematical expression that defines the quantity to be maximized or minimized within a given set of constraints. In optimization problems, this function is evaluated at various points within the feasible region to determine the best possible outcome. Recognizing how to formulate and analyze the objective function is crucial for solving these types of problems.
Recommended video:
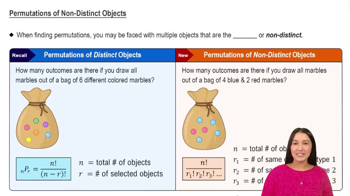
Permutations of Non-Distinct Objects
Piecewise Functions
A piecewise function is defined by different expressions based on the input value, often used to model situations where a rule changes at certain points. Understanding how to interpret and graph piecewise functions is important, especially when determining the maximum or minimum values, as the function's behavior can vary significantly across different intervals.
Recommended video:
 Verified Solution
Verified Solution


 7:2m
7:2m
