Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
5. Rational Functions
Asymptotes
Problem 47
Textbook Question
In Exercises 45–56, use transformations of f(x)=1/x or f(x)=1/x^2 to graph each rational function. h(x)=1/x + 2
 Verified step by step guidance
Verified step by step guidance1
Identify the base function: The base function here is \( f(x) = \frac{1}{x} \).
Determine the transformation: The function \( h(x) = \frac{1}{x} + 2 \) is a vertical shift of the base function \( f(x) = \frac{1}{x} \) by 2 units upwards.
Graph the base function: Start by sketching the graph of \( f(x) = \frac{1}{x} \), which is a hyperbola with vertical and horizontal asymptotes at \( x = 0 \) and \( y = 0 \), respectively.
Apply the transformation: Shift the entire graph of \( f(x) = \frac{1}{x} \) upwards by 2 units. This means the horizontal asymptote will now be at \( y = 2 \) instead of \( y = 0 \).
Sketch the transformed graph: Draw the new graph of \( h(x) = \frac{1}{x} + 2 \) with the asymptotes at \( x = 0 \) and \( y = 2 \), ensuring the hyperbola is shifted upwards accordingly.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Rational Functions
Rational functions are expressions formed by the ratio of two polynomials. They can exhibit unique behaviors such as asymptotes, intercepts, and discontinuities. Understanding the basic structure of rational functions is essential for analyzing their graphs and transformations.
Recommended video:

Intro to Rational Functions
Transformations of Functions
Transformations involve shifting, stretching, compressing, or reflecting the graph of a function. For example, adding a constant to a function, like in h(x) = 1/x + 2, translates the graph vertically. Recognizing how these transformations affect the original function is crucial for accurately graphing the new function.
Recommended video:

Domain & Range of Transformed Functions
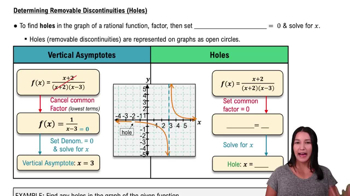
Asymptotes
Asymptotes are lines that a graph approaches but never touches. For rational functions, vertical asymptotes occur where the denominator is zero, while horizontal asymptotes indicate the behavior of the function as x approaches infinity. Identifying these asymptotes helps in sketching the graph and understanding its limits.
Recommended video:

Introduction to Asymptotes

 6:24m
6:24mWatch next
Master Introduction to Asymptotes with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice