Find the slope of the line satisfying the given conditions. See Example 5. vertical, through (4, -7)

Key Concepts

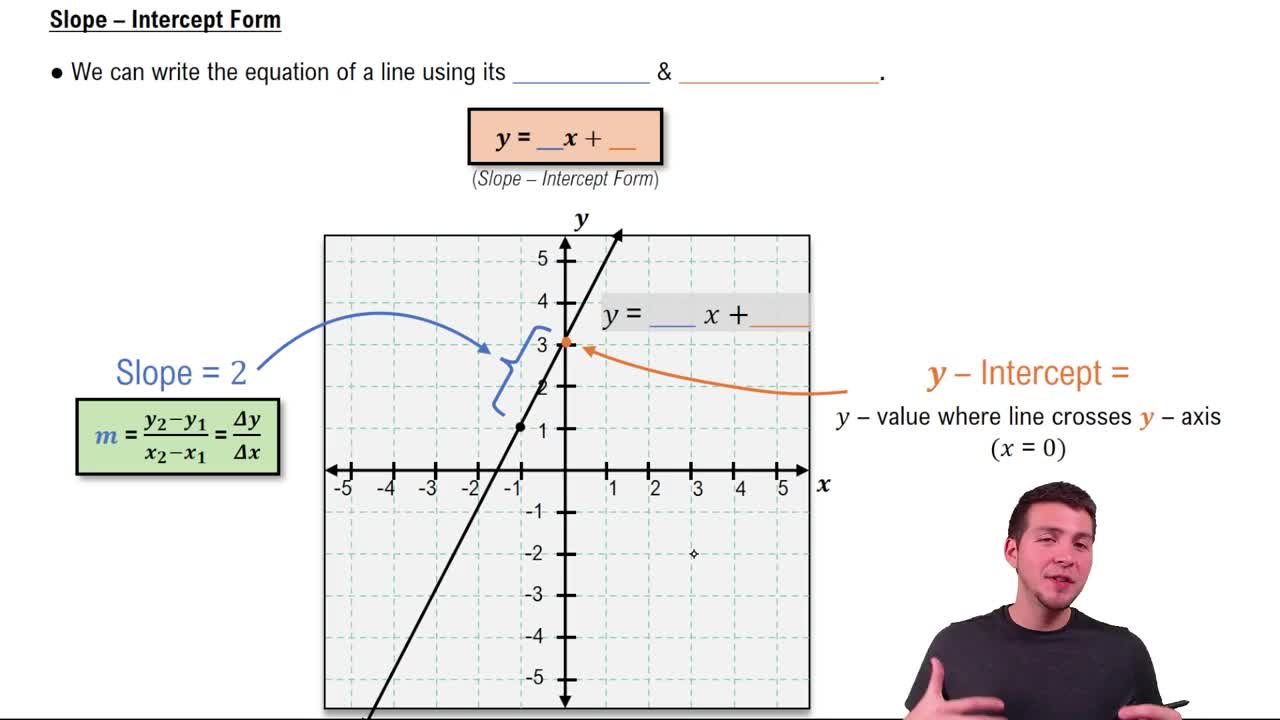
Slope of a Line

The slope of a line is a measure of its steepness, typically represented as 'm' in the slope-intercept form of a linear equation, y = mx + b. It is calculated as the ratio of the change in the y-coordinates to the change in the x-coordinates between two points on the line. A positive slope indicates the line rises as it moves from left to right, while a negative slope indicates it falls.

Vertical Lines

A vertical line is a line that goes straight up and down, having an undefined slope. This occurs because the change in x-coordinates is zero, leading to a division by zero when calculating slope. Vertical lines are represented by equations of the form x = a, where 'a' is a constant, indicating that all points on the line have the same x-coordinate.

Point-Slope Form

The point-slope form of a linear equation is used to express the equation of a line given a point on the line and its slope. It is written as y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope. This form is particularly useful for quickly writing the equation of a line when the slope and a point are known.