Use the graph to solve each equation or inequality. Use interval ...

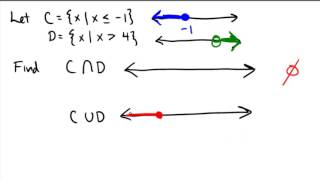
Question

Use the graph to solve each equation or inequality. Use interval notation where appropriate. 2(X-2) / {(X-1)(X-3)} > 0

Graph of the inequality 2(X-2) / ((X-1)(X-3)) > 0 on a coordinate plane.

Accepted Answer

Hey, everyone in this problem, we're asked to find a solution for the following inequality. And the inequality we're given is three multiplied by X minus five, all divided by X minus four, multiplied by X minus six is greater than zero. We're told to solve that using the graph of F of X equals three multiplied by X minus five, divided by X minus four, multiplied by X minus six, which is given below. And we're told to express the answer in interval notation. So given the graph of the function F FX, it's drawn in red here and we have four answer choices as well. Now the answer choices are the union of two intervals. For options, A through D, the second interval is from six to positive infinity. For each of those choices. The first interval for option A is from negative 5 to 4. For B it's negative infinity to five or C, it's 4 to 5. And for D it's negative 4 to 5 and none of the intervals use square brackets. They all use round brackets to indicate that they are not including the end points. So let's get started here. We are going to write the inequality, we have three multiplied by X minus five, divided by X minus four, multiplied by X minus six. And that is greater than zero. Now, if we compare this to the graph, we're giving OK, the graph of the function F of X, well, F of X is the exact same as what we have on the left hand side of our inequality. So the inequality we're trying to solve is actually F of X is greater than zero. Now, when we're given the graph of F FX, OK. Recall that F FX is represented by the Y value or on the Y axis. So what we really want is Y greater than zero, which means that we wanna look above the X axis. OK? What X values give us a Y value that's above the X axis. And we're gonna trace all the Y values that do that. So we can see that just after four, we have our first positive Y value that continues until five K X equals five. The function is equal to zero and then it continues downwards into the negative values. And then again, at six, just after six, we get this positive function value and that's gonna continue until infinity. So we're running out this interval. The first positive value of F FX is when X is equal to four. So we start our interval at four. Now at four, it looks like we have a vertical Asymptote. OK. There is no function value at four. The function is not defined. So we have a round bracket there because we can't include that point. This stays positive until X is equal to five. OK. And we're gonna use a round bracket here as well because at X equals five, the function F of X is equal to zero, our inequality is strictly greater. Then we don't want to include the values where it's equal to. So we use a round bracket there and then we have the union of the next interval. And again, just like at four, we have this vertical ascent tode at X equals six, we get positive values starting from six, but not including it. And those continue all the way up to infinity. And we can see that this function is going to approach the horizontal axis but it is gonna remain positive. And so the union of those two intervals is our total or full solution. If we compare this to our answer choices, we can see that this corresponds with answer choice. C thanks everyone for watching. I hope this video helped see you in the next one.

Use the graph to solve each equation or inequality. Use interval notation where appropriate. 2(X-2) / {(X-1)(X-3)} > 0

Key Concepts

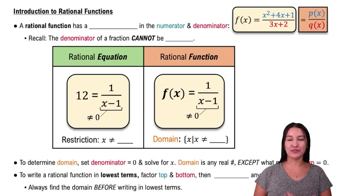
Rational Functions

Inequalities and Interval Notation

Graph Analysis

Watch next