Table of contents

0. Review of Algebra4h 16m
1. Equations & Inequalities3h 18m
2. Graphs of Equations43m
3. Functions2h 17m
4. Polynomial Functions1h 44m
5. Rational Functions1h 23m
6. Exponential & Logarithmic Functions2h 28m
7. Systems of Equations & Matrices4h 6m
8. Conic Sections2h 23m
9. Sequences, Series, & Induction1h 19m
10. Combinatorics & Probability1h 45m

1. Equations & Inequalities

Linear Inequalities

College Algebra

1. Equations & Inequalities

Linear Inequalities

Previous problemNext problem

0:59 minutes

Problem 2a

Textbook Question

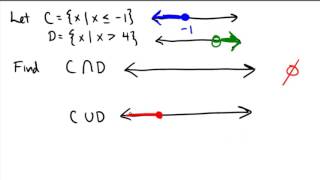
Match each equation or inequality in Column I with the graph of its solution set in Column II. | x | = -7

Verified step by step guidance

Step 1: Understand the absolute value concept. The absolute value of a number, denoted as |x|, represents its distance from zero on the number line, which is always non-negative.

Step 2: Analyze the given equation |x| = -7. Since absolute values are always non-negative, they cannot equal a negative number.

Step 3: Conclude that there is no real number x that satisfies the equation |x| = -7.

Step 4: Recognize that the solution set for this equation is the empty set, meaning there are no solutions.

Step 5: Match this understanding with the graph in Column II that represents an empty solution set, typically shown as no points on the number line.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

59s

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Absolute Value

The absolute value of a number is its distance from zero on the number line, regardless of direction. It is denoted by vertical bars, such as |x|. For example, |3| = 3 and |-3| = 3. In the context of equations, |x| = a means x can be either a or -a, provided a is non-negative.

No Solution in Absolute Value Equations

An absolute value equation like |x| = -7 has no solution because the absolute value cannot be negative. The definition of absolute value ensures that it is always zero or positive, thus making it impossible for |x| to equal a negative number. This concept is crucial for understanding the limitations of absolute value equations.

Graphing Absolute Value Functions

The graph of an absolute value function, such as y = |x|, forms a 'V' shape, opening upwards. The vertex of the graph is at the origin (0,0), and it reflects symmetrically across the y-axis. Understanding how to graph these functions helps visualize the solution sets of absolute value equations and inequalities.