Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
7. Systems of Equations & Matrices
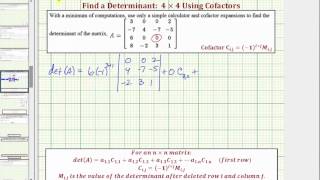
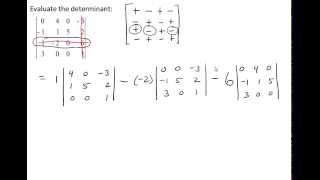
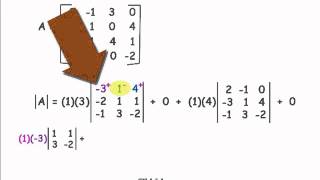
Determinants and Cramer's Rule
Problem 23c
Textbook Question
Textbook QuestionFind the inverse, if it exists, for each matrix. [3x3 matrix]
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
9mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Matrix Inversion
Matrix inversion is the process of finding a matrix that, when multiplied with the original matrix, yields the identity matrix. For a square matrix A, the inverse is denoted as A⁻¹, and it exists only if the matrix is non-singular, meaning its determinant is non-zero. The inverse is crucial in solving systems of linear equations and in various applications across mathematics and engineering.
Recommended video:

Graphing Logarithmic Functions
Determinant
The determinant is a scalar value that provides important information about a matrix, including whether it is invertible. For a 3x3 matrix, the determinant can be calculated using a specific formula involving the elements of the matrix. If the determinant is zero, the matrix is singular and does not have an inverse; if it is non-zero, the matrix is invertible.
Recommended video:
Guided course

Determinants of 2×2 Matrices
Identity Matrix
The identity matrix is a special type of square matrix that has ones on the diagonal and zeros elsewhere. It acts as the multiplicative identity in matrix multiplication, meaning that any matrix multiplied by the identity matrix remains unchanged. The identity matrix is essential in defining the concept of matrix inverses, as the product of a matrix and its inverse results in the identity matrix.
Recommended video:
Guided course

Introduction to Matrices

 4:36m
4:36mWatch next
Master Determinants of 2×2 Matrices with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice