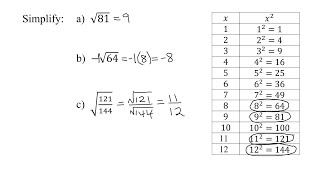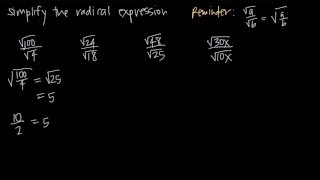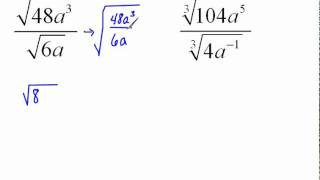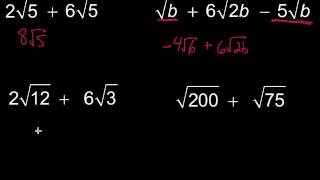Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Radical Expressions
Problem 143
Textbook Question
Textbook QuestionSolve for x: ∛(x√x) = 9
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Radical Expressions
Radical expressions involve roots, such as square roots or cube roots. In the given equation, the cube root of a product is present, which requires understanding how to manipulate and simplify expressions involving radicals. Recognizing how to isolate the radical and eliminate it through exponentiation is crucial for solving the equation.
Recommended video:
Guided course

Radical Expressions with Fractions
Exponents and Powers
Exponents represent repeated multiplication of a number by itself. In this problem, understanding how to apply the properties of exponents is essential, especially when dealing with roots. For instance, the cube root can be expressed as raising to the power of one-third, which allows for easier manipulation of the equation.
Recommended video:

Powers of i
Solving Equations
Solving equations involves finding the value of the variable that makes the equation true. This requires isolating the variable through various algebraic techniques, such as adding, subtracting, multiplying, or dividing both sides of the equation. In this case, after simplifying the radical expression, one must carefully perform operations to isolate x and find its value.
Recommended video:

Solving Logarithmic Equations
Related Videos
Related Practice