Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Intro to Functions & Their Graphs
Problem 66
Textbook Question
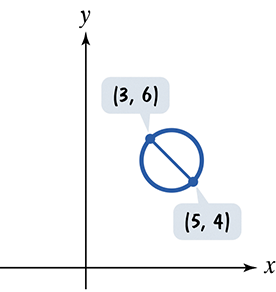
In Exercises 65-66, a line segment through the center of each circle intersects the circle at the points shown.
a. Find the coordinates of the circle's center.
b. Find the radius of the circle.
c. Use your answers from parts (a) and (b) to write the standard form of the circle's equation. 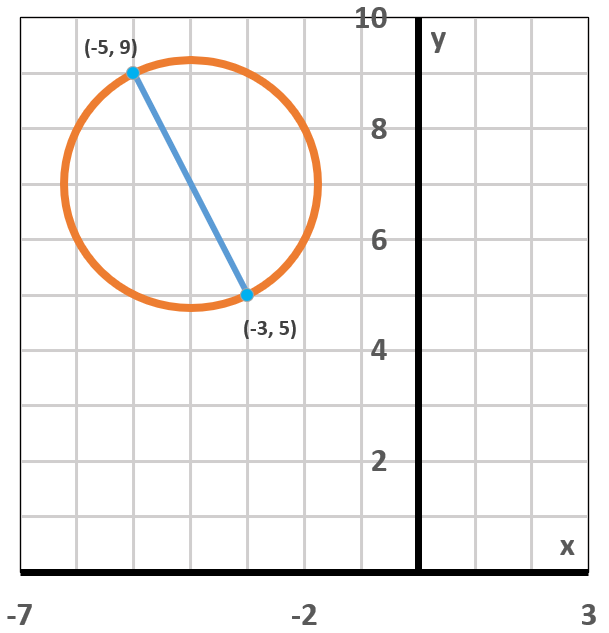
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the coordinates of the endpoints of the diameter. For the first circle, the endpoints are (-5, 9) and (-3, 5). For the second circle, the endpoints are (3, 6) and (5, 4).
Step 2: Calculate the midpoint of the diameter to find the center of the circle. Use the midpoint formula: \( \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) \).
Step 3: Apply the midpoint formula to the endpoints of the first circle: \( \left( \frac{-5 + (-3)}{2}, \frac{9 + 5}{2} \right) \). Apply the midpoint formula to the endpoints of the second circle: \( \left( \frac{3 + 5}{2}, \frac{6 + 4}{2} \right) \).
Step 4: Calculate the radius of the circle. Use the distance formula to find the distance between the center and one of the endpoints: \( \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
Step 5: Write the standard form of the circle's equation using the center (h, k) and radius r: \( (x - h)^2 + (y - k)^2 = r^2 \).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?

 5:2m
5:2mWatch next
Master Relations and Functions with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice






