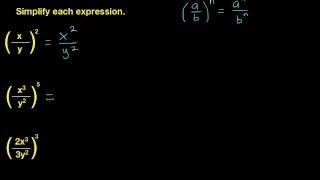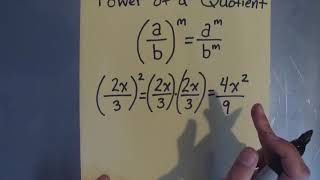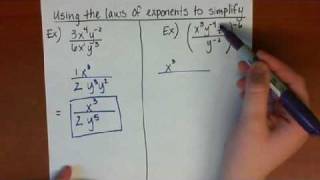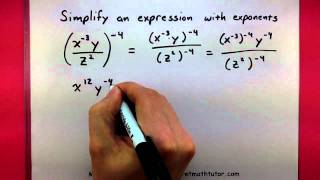Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Exponents
Problem 102a
Textbook Question
Let U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}, M = {0, 2, 4, 6, 8}, N = {1, 3, 5, 7, 9, 11, 13}, Q = {0, 2, 4, 6, 8, 10, 12}, and R = {0, 1, 2, 3, 4}.Use these sets to find each of the following. Identify any disjoint sets. Q ∩ (M ∪ N)
 Verified step by step guidance
Verified step by step guidance1
Identify the sets involved: M = \{0, 2, 4, 6, 8\}, N = \{1, 3, 5, 7, 9, 11, 13\}, and Q = \{0, 2, 4, 6, 8, 10, 12\}.
Find the union of sets M and N, denoted as M \cup N. This involves combining all elements from both sets without repeating any elements.
Calculate M \cup N = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13\}.
Find the intersection of set Q with the result from the previous step, M \cup N. This is denoted as Q \cap (M \cup N).
Calculate Q \cap (M \cup N) by identifying the common elements between Q and M \cup N.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Set Operations
Set operations are fundamental actions that can be performed on sets, including union, intersection, and difference. The union of two sets combines all elements from both sets, while the intersection includes only the elements common to both sets. Understanding these operations is crucial for manipulating and analyzing sets effectively.
Recommended video:
Guided course

Performing Row Operations on Matrices
Disjoint Sets
Disjoint sets are sets that have no elements in common, meaning their intersection is the empty set. Identifying disjoint sets is important in various mathematical contexts, as it helps in understanding relationships between different groups of elements. In this question, recognizing disjoint sets can simplify the analysis of the given sets.
Recommended video:

Interval Notation
Universal Set
The universal set is the set that contains all possible elements relevant to a particular discussion or problem. In this context, U represents the universal set, which includes all integers from 0 to 13. Understanding the universal set is essential for determining the relationships and operations involving subsets, such as M, N, Q, and R.
Recommended video:

Interval Notation

 7:39m
7:39mWatch next
Master Introduction to Exponent Rules with a bite sized video explanation from Patrick Ford
Start learningRelated Videos
Related Practice