In Exercises 1-16, use the graph of y = f(x) to graph each function g.
g(x) = 2f(x)

Key Concepts

Function Transformation

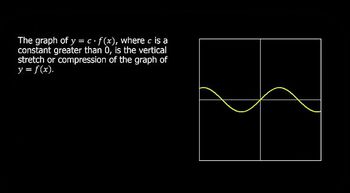
Function transformation refers to the process of altering the graph of a function through various operations, such as vertical or horizontal shifts, stretches, or reflections. In this case, the function g(x) = 2f(x) represents a vertical stretch of the original function f(x) by a factor of 2, which means that all y-values of f(x) will be multiplied by 2.

Graphing Functions

Graphing functions involves plotting points on a coordinate plane to visually represent the relationship between the input (x) and output (y) values of a function. For the function g(x) = 2f(x), one must first understand the graph of f(x) and then apply the transformation to create the graph of g(x), ensuring that the new points reflect the vertical stretch.

Horizontal Line Test

The horizontal line test is a method used to determine if a function is one-to-one, meaning that each output value corresponds to exactly one input value. In the context of the given graph, since f(x) is a horizontal line, it fails the horizontal line test, indicating that it is not a one-to-one function. However, this characteristic does not affect the transformation to g(x) but is important for understanding the nature of f(x).