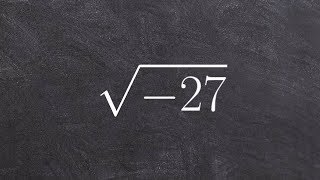Find each product or quotient. Simplify the answers. √-6 * √-2 / √3

Key Concepts

Imaginary Numbers

Imaginary numbers are defined as multiples of the imaginary unit 'i', where i is the square root of -1. In this problem, the square roots of negative numbers, such as √-6 and √-2, can be expressed as i√6 and i√2, respectively. Understanding how to manipulate imaginary numbers is crucial for simplifying expressions involving square roots of negative values.

Properties of Square Roots

The properties of square roots state that √a * √b = √(a*b) and √a / √b = √(a/b), provided a and b are non-negative. When dealing with negative numbers, these properties still apply, but we must incorporate the imaginary unit. This concept is essential for simplifying the products and quotients of square roots in the given expression.

Simplification of Complex Expressions

Simplifying complex expressions involves combining like terms, reducing fractions, and applying algebraic rules. In this case, after substituting the imaginary components and applying the properties of square roots, one must simplify the resulting expression to its simplest form. This process is vital for arriving at a clear and concise answer.