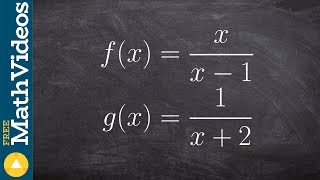Use a graphing calculator to graph each equation in the standard viewing window. y = 3x + 4

Verified step by step guidance

1. Identify the equation of the line: \( y = 3x + 4 \). This is in the slope-intercept form \( y = mx + b \), where \( m \) is the slope and \( b \) is the y-intercept.
2. Determine the slope \( m \) and y-intercept \( b \) from the equation. Here, \( m = 3 \) and \( b = 4 \).
3. Plot the y-intercept on the graph. Since \( b = 4 \), place a point at \( (0, 4) \) on the y-axis.
4. Use the slope \( m = 3 \) to find another point. The slope \( 3 \) means rise over run is \( \frac{3}{1} \). From the y-intercept \( (0, 4) \), move up 3 units and 1 unit to the right to plot the next point.
5. Draw a straight line through the points \( (0, 4) \) and the new point. This line represents the graph of the equation \( y = 3x + 4 \).

Key Concepts

Linear Equations

A linear equation is an algebraic expression that represents a straight line when graphed on a coordinate plane. It is typically written in the form y = mx + b, where m is the slope and b is the y-intercept. In the equation y = 3x + 4, the slope is 3, indicating the line rises three units for every one unit it moves to the right, while the y-intercept is 4, meaning the line crosses the y-axis at (0, 4).

Graphing Calculators

A graphing calculator is a powerful tool that allows users to visualize mathematical functions and equations. It can plot graphs, perform calculations, and analyze data. To graph the equation y = 3x + 4, one would input the equation into the calculator, which will then display the corresponding line on the graph, helping to understand the relationship between x and y values.

Standard Viewing Window

The standard viewing window on a graphing calculator typically displays the range of x-values from -10 to 10 and y-values from -10 to 10. This window is useful for visualizing most linear equations, as it provides a balanced view of the graph. Adjusting the viewing window can help in analyzing specific features of the graph, such as intercepts and slopes, ensuring that the entire line is visible.