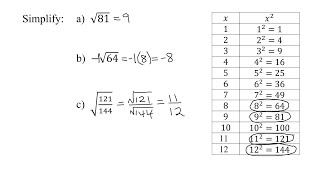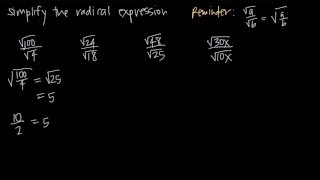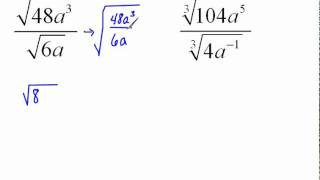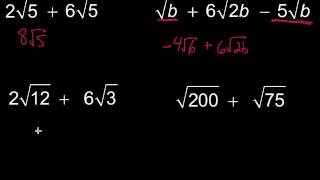In Exercises 50 - 53, rationalize the denominator. 30/√5

Key Concepts

Rationalizing the Denominator

Rationalizing the denominator involves eliminating any irrational numbers from the denominator of a fraction. This is typically achieved by multiplying both the numerator and the denominator by a suitable expression that will result in a rational number in the denominator. For example, to rationalize 30/√5, you would multiply by √5/√5.

Irrational Numbers

Irrational numbers are numbers that cannot be expressed as a simple fraction, meaning they cannot be written as the ratio of two integers. Common examples include square roots of non-perfect squares, such as √2 or √5. In the context of rationalizing denominators, the presence of an irrational number in the denominator is what necessitates the rationalization process.

Multiplication of Fractions

Multiplication of fractions involves multiplying the numerators together and the denominators together. When rationalizing a denominator, this principle is applied to ensure that the fraction remains equivalent after multiplying by a form of one (like √5/√5). This step is crucial for maintaining the value of the original expression while transforming its form.