In Exercises 53-66, begin by graphing the standard quadratic function, f(x) = x². Then use transformations of this graph to graph the given function. h(x) = (1/2) (x − 1)² – 1

Key Concepts

Quadratic Functions

A quadratic function is a polynomial function of degree two, typically expressed in the form f(x) = ax² + bx + c. The graph of a quadratic function is a parabola, which opens upwards if 'a' is positive and downwards if 'a' is negative. Understanding the basic shape and properties of the standard quadratic function, f(x) = x², is essential for applying transformations to graph other quadratic functions.

Transformations of Functions

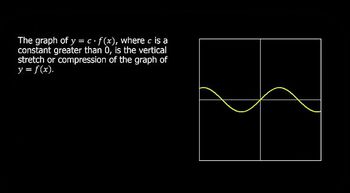
Transformations of functions involve shifting, stretching, compressing, or reflecting the graph of a function. For quadratic functions, common transformations include vertical shifts (adding or subtracting a constant), horizontal shifts (adding or subtracting from the input), and vertical stretches or compressions (multiplying by a constant). In the given function h(x) = (1/2)(x − 1)² – 1, the transformations applied to f(x) = x² include a horizontal shift to the right and a vertical compression.

Vertex Form of a Quadratic Function

The vertex form of a quadratic function is expressed as f(x) = a(x - h)² + k, where (h, k) is the vertex of the parabola. This form makes it easier to identify the vertex and understand the transformations applied to the standard quadratic function. In the function h(x) = (1/2)(x − 1)² – 1, the vertex is at (1, -1), indicating the point where the parabola reaches its minimum value, which is crucial for accurately graphing the function.