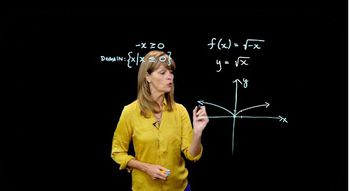Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Transformations
Problem 31
Textbook Question
Graph each function. See Examples 1 and 2. h(x)=√(4x)
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the parent function. The parent function in this case is f(x) = √x. This is a basic square root function, which starts at the origin (0,0) and increases as x increases.
Step 2: Identify any transformations. In this case, the function is h(x) = √(4x), which is a horizontal compression of the parent function by a factor of 1/4. This means the graph will be 'narrower' than the parent function.
Step 3: Plot the parent function. Start by plotting the point (0,0). Then, as x increases, the y-value will be the square root of x. For example, when x=1, y=√1=1. When x=4, y=√4=2, and so on.
Step 4: Apply the transformation to the parent function. Since we have a horizontal compression by a factor of 1/4, each x-value in the parent function will be divided by 4 in the transformed function. For example, the point (1,1) on the parent function will become (1/4,1) on the transformed function.
Step 5: Connect the points to form the graph of the function h(x) = √(4x). The graph should start at the origin and increase as x increases, but it should be 'narrower' than the graph of the parent function due to the horizontal compression.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
8mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Square Root Function
The square root function, denoted as √x, is a fundamental mathematical function that returns the non-negative value whose square equals x. It is defined for all non-negative real numbers and has a characteristic 'half-parabola' shape when graphed. Understanding this function is crucial for analyzing the behavior of h(x) = √(4x), particularly its domain and range.
Recommended video:

Imaginary Roots with the Square Root Property
Transformation of Functions
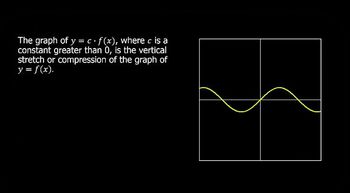
Transformation of functions involves altering the graph of a parent function through shifts, stretches, or reflections. In the case of h(x) = √(4x), the factor of 4 indicates a vertical stretch of the square root function. Recognizing how these transformations affect the graph is essential for accurately plotting the function.
Recommended video:

Domain & Range of Transformed Functions
Domain and Range
The domain of a function refers to the set of all possible input values (x-values) for which the function is defined, while the range is the set of all possible output values (y-values). For h(x) = √(4x), the domain is x ≥ 0, since the square root is only defined for non-negative inputs, and the range is also y ≥ 0, as square roots yield non-negative outputs. Understanding these concepts is vital for graphing the function correctly.
Recommended video:

Domain & Range of Transformed Functions

 5:25m
5:25mWatch next
Master Intro to Transformations with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice