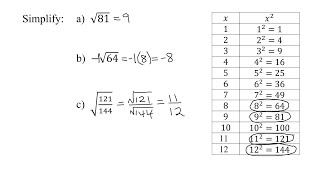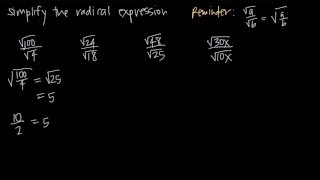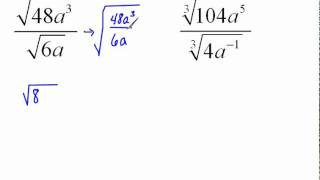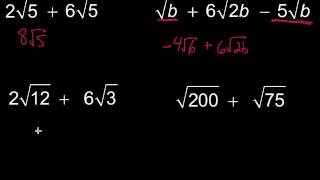Table of contents

0. Review of Algebra4h 16m
1. Equations & Inequalities3h 18m
2. Graphs of Equations43m
3. Functions2h 17m
4. Polynomial Functions1h 44m
5. Rational Functions1h 23m
6. Exponential & Logarithmic Functions2h 28m
7. Systems of Equations & Matrices4h 6m
8. Conic Sections2h 23m
9. Sequences, Series, & Induction1h 19m
10. Combinatorics & Probability1h 45m

0. Review of Algebra

Radical Expressions

College Algebra

0. Review of Algebra

Radical Expressions

1:39 minutes

Problem 79a

Textbook Question

Evaluate each expression. See Example 7. (-4)^1/2

Verified Solution

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Exponents

Exponents represent repeated multiplication of a number by itself. In the expression (-4)^(1/2), the exponent 1/2 indicates the square root of the base, which is -4. Understanding how to manipulate exponents is crucial for evaluating expressions involving powers and roots.

Square Roots of Negative Numbers

The square root of a negative number is not defined within the set of real numbers; instead, it leads to complex numbers. For example, the square root of -4 can be expressed as 2i, where 'i' is the imaginary unit. This concept is essential for correctly evaluating expressions that involve negative bases raised to fractional exponents.

Complex Numbers

Complex numbers are numbers that have a real part and an imaginary part, typically expressed in the form a + bi, where 'a' is the real part and 'b' is the coefficient of the imaginary unit 'i'. Understanding complex numbers is vital when dealing with expressions that yield non-real results, such as the square root of negative numbers.