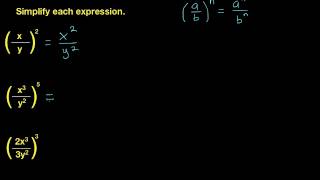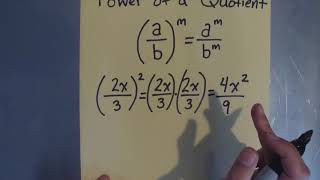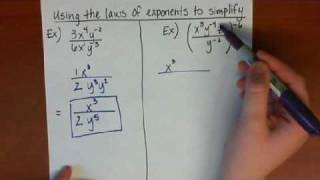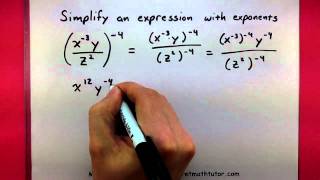In Exercises 75–84, state the name of the property illustrated. 1/(x+3) (x+3)=1, x≠−3

Key Concepts

Multiplicative Inverse Property

The Multiplicative Inverse Property states that for any non-zero number 'a', the product of 'a' and its multiplicative inverse (1/a) equals 1. In the given expression, (1/(x+3))(x+3) demonstrates this property, as the term (x+3) acts as the inverse of 1/(x+3), resulting in a product of 1, provided x is not equal to -3.

Domain Restrictions

Domain restrictions refer to the values that a variable cannot take in a mathematical expression. In this case, x cannot equal -3 because it would make the denominator zero, leading to an undefined expression. Understanding domain restrictions is crucial for ensuring that mathematical operations are valid and do not result in undefined behavior.

Identity Element

The identity element in multiplication is the number 1, as multiplying any number by 1 leaves it unchanged. In the context of the expression (1/(x+3))(x+3)=1, the result of the multiplication illustrates that the product of a number and its multiplicative inverse yields the identity element, reinforcing the foundational concept of identity in algebra.