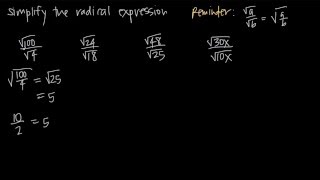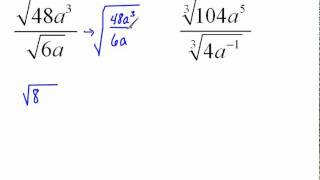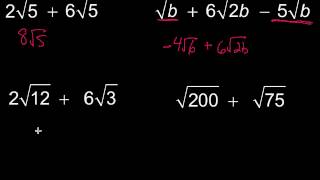Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
0. Review of Algebra
Radical Expressions
Problem 44a
Textbook Question
Find each root. ∜(5 + 2m)⁴
 Verified step by step guidance
Verified step by step guidance1
Recognize that the expression given is ∜{(5 + 2m)^4}. This is a fourth root of a power.
Understand that taking the fourth root of something raised to the fourth power will simplify the expression. In general, ∜{x^4} = x, assuming x is non-negative.
Apply this property to the expression: ∜{(5 + 2m)^4} simplifies to 5 + 2m.
Verify that the simplification is valid by considering the domain of the expression. Since we are dealing with real numbers, ensure that 5 + 2m is non-negative.
Conclude that the root of the expression is simply the base of the power, which is 5 + 2m, under the assumption that it is non-negative.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Roots and Radicals
Roots and radicals involve the operation of extracting a root from a number or expression. The nth root of a number 'a' is a value 'b' such that b^n = a. In this context, the fourth root (∜) indicates that we are looking for a number that, when raised to the fourth power, equals the expression inside the radical.
Recommended video:
Guided course

Expanding Radicals
Exponents and Powers
Exponents represent repeated multiplication of a base number. For example, in (5 + 2m)⁴, the expression is raised to the fourth power, meaning (5 + 2m) is multiplied by itself four times. Understanding how to manipulate exponents is crucial for simplifying expressions and solving equations involving powers.
Recommended video:

Powers of i
Simplifying Expressions
Simplifying expressions involves reducing them to their most basic form while maintaining equivalence. This includes combining like terms, applying the distributive property, and reducing fractions. In the given problem, simplifying (5 + 2m)⁴ before taking the fourth root is essential for finding the roots accurately.
Recommended video:
Guided course

Simplifying Algebraic Expressions
Related Videos
Related Practice