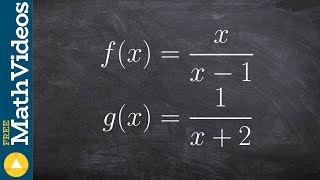Table of contents
- 0. Review of Algebra4h 16m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 6m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 19m
- 10. Combinatorics & Probability1h 45m
3. Functions
Function Composition
Problem 83a
Textbook Question
Textbook QuestionIn Exercises 82–84, find f + g, f - g, fg, and f/g. f(x) = x^2 + x + 1, g(x) = x^2 -1
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Function Addition and Subtraction
Function addition and subtraction involve combining two functions by adding or subtracting their outputs for the same input value. For example, if f(x) = x^2 + x + 1 and g(x) = x^2 - 1, then (f + g)(x) = f(x) + g(x) and (f - g)(x) = f(x) - g(x). This process requires careful algebraic manipulation to combine like terms.
Recommended video:

Adding & Subtracting Functions
Function Multiplication
Function multiplication entails multiplying the outputs of two functions for the same input. For the functions f(x) and g(x), the product is defined as (fg)(x) = f(x) * g(x). This operation often results in a polynomial that can be simplified by distributing the terms and combining like terms, which is essential for further analysis.
Recommended video:

Finding Zeros & Their Multiplicity
Function Division
Function division involves dividing the output of one function by another for the same input. For f(x) and g(x), the quotient is expressed as (f/g)(x) = f(x) / g(x). It is important to note that division by zero is undefined, so one must ensure that g(x) does not equal zero for the values of x being considered.
Recommended video:

Multiplying & Dividing Functions

 4:56m
4:56mWatch next
Master Function Composition with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice