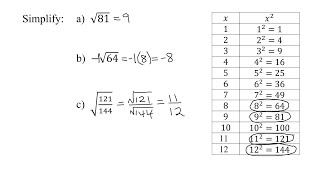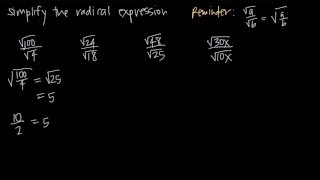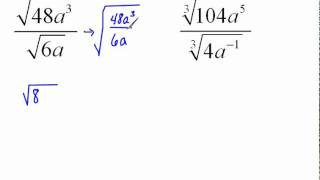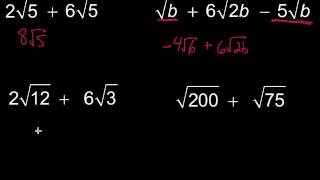In Exercises 1–20, evaluate each expression, or state that the expression is not a real number. ____ √0.81

Key Concepts

Square Roots

The square root of a number 'x' is a value 'y' such that y² = x. For non-negative numbers, every positive number has two square roots: one positive and one negative. However, the square root of zero is uniquely zero, as 0² = 0. Understanding square roots is essential for evaluating expressions involving radical signs.

Real Numbers

Real numbers include all the numbers on the number line, encompassing rational numbers (like integers and fractions) and irrational numbers (like √2 and π). When evaluating expressions, it's important to determine if the result is a real number, as some operations may yield complex or undefined results. In this case, the square root of a non-negative number will always yield a real number.

Evaluating Expressions

Evaluating an expression involves substituting values into the expression and simplifying it to find a numerical result. In the context of square roots, this means calculating the principal square root of a given number. For example, evaluating √0.81 requires recognizing that 0.81 is a perfect square, leading to a straightforward calculation of its square root.