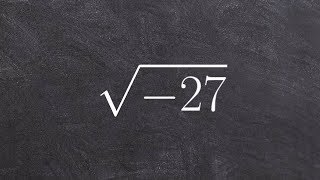In Exercises 95–99, perform the indicated operations and write the result in standard form. (i^98 - i^94)/i^49

Key Concepts

Complex Numbers

Complex numbers are numbers that have a real part and an imaginary part, typically expressed in the form a + bi, where 'a' is the real part and 'b' is the coefficient of the imaginary unit 'i'. The imaginary unit 'i' is defined as the square root of -1, which allows for the extension of the number system to include solutions to equations that do not have real solutions.

Powers of i

The powers of the imaginary unit 'i' follow a cyclical pattern: i^1 = i, i^2 = -1, i^3 = -i, and i^4 = 1. This cycle repeats every four powers, meaning that any power of 'i' can be simplified by reducing the exponent modulo 4. Understanding this pattern is crucial for simplifying expressions involving powers of 'i'.

Standard Form of Complex Numbers

The standard form of a complex number is expressed as a + bi, where 'a' and 'b' are real numbers. To write a complex number in standard form, one must combine like terms and ensure that the imaginary unit 'i' is clearly separated from the real part. This form is essential for performing operations such as addition, subtraction, and multiplication of complex numbers.